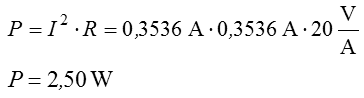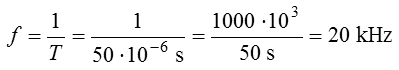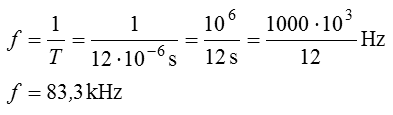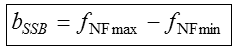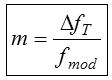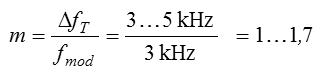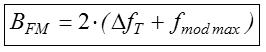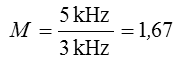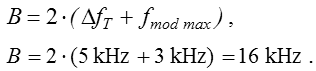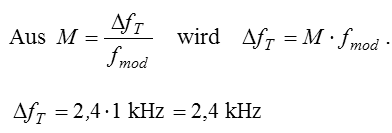Lehrgang nach dem neuen Fragenkatalog vom 28.2.2007

Um in der Funktechnik eine Information, zum Beispiel Sprache, Ton, Bild, Daten von einem Ort zu einem anderen übertragen zu können, wandelt man diese zunächst in elektrische Größen um, meistens in eine Spannung. Diese elektrischen Größen nennt man Signale.

• Sinusförmige Signale
• Signale auf dem Oszilloskop
• Die Zeigerdarstellung
• Nichtsinusförmige Signale
• Nicht-periodische Signale
• Modulierte Signale
• Doppelseitenbandmodulation
• Amplitudenmodulation
• Einseitenbandmodulation(SSB)
• Frequenzmodulation
• Die Besselfunktion
• Modulierte Signale mit Hilfsträger
• Kennzeichnung der Sendearten

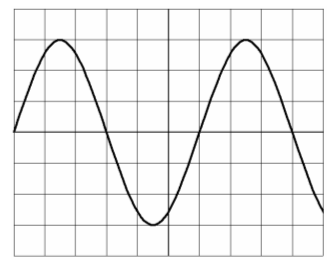
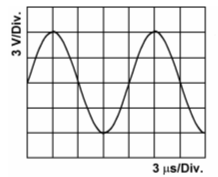
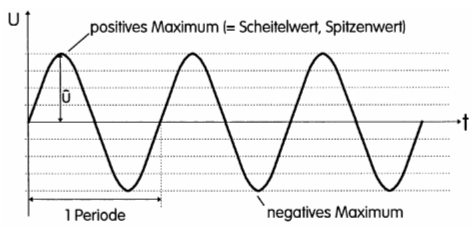
Wandelt man den Schalldruck von Sprache über ein Mikrofon in elektrische Spannung um, entstehen analoge Signale. Analoge Signale überträgt man in der Funktechnik durch Modulation auf einen Träger (modulierte Signale). Ein Träger ist eine hochfrequente sinusförmige Wechselspannung. Auch modulierte Träger gehören zum Thema „Signale“.

Auch Spannungen, die nach einem bestimmten System (zum Beispiel Morsecode, Baudot-Code in RTTY) ein- und ausgeschaltet werden, enthalten Informationen. Man nennt diese Signale digitale Signale.

Eine sinusförmige Spannung entsteht auf „natürliche“ Art, indem man eine Spule in einem Magnetfeld sich drehen lässt und an den Klemmen die induzierte Spannung abnimmt. Man nennt diese Art der sinusförmigen Spannungserzeugung „Wechselspannungsgenerator“. Sie wird in der Energietechnik angewendet. In der Hochfrequenztechnik erzeugt man sinusförmige Spannungen mit Hilfe von Oszillatoren (siehe Lektion 7). Eine sinusförmige Spannung hat folgenden Verlauf.

Bild 11-1: Sinusförmiges Signal

Man definiert den höchsten Wert als Scheitelwert oder Spitzenwert und eine vollständige Schwingung als Periode. Die Spannung vom positiven Maximum bis zum negativen Maximum heißt Spitze-Spitze-Wert. In der Wechselstromtechnik spielt noch der Effektivwert eine wichtige Rolle. Die Anzahl der Schwingungen pro Zeiteinheit ist die Frequenz. Diese Begriffe wurden bereits in der Lektion 2 im Amateurfunklehrgang zur Klasse E erläutert. Dazu gibt es auch in der Prüfung zum Amateurfunkzeugnis Klasse A eine Reihe Prüfungsfragen im Fragenkatalog.

Prüfungsfrage

TB601  Welche der im folgenden Diagramm eingezeichneten Gleichspannungen (U1 ... U6) setzen an einem Wirkwiderstand die gleiche Leistung um wie die dargestellte sinusförmige Wechselspannung?
	U2 oder U5
	U1 oder U6
	U3 oder U4
	nur U2

Prüfungsfrage

TB607  Ein sinusförmiges Signal hat einen Effektivwert von 12 Volt. Wie groß ist der Spitze-Spitze-Wert?
	16,97
	33,9 V
	24 V
	36,4 V

Lösung: Zunächst berechnen Sie den Spitzen- oder Scheitelwert aus dem gegebenen Effektivwert.

û = √2 · 12 V = 16,97 V

Der Spitze-Spitze-Wert ist doppelt so groß wie der einfache Spitzenwert. Also multiplizieren Sie diesen Wert mit zwei und Sie haben die Lösung.

Prüfungsfrage

TB608  Der Spitzenwert der häuslichen 230-V-Stromversorgung beträgt
	163 Volt
	325 Volt
	460 Volt
	650 Volt

Lösung:  û = √2 · 230 V = 325 V

Prüfungsfrage

TB609  Der Spitzen-Spitzen-Wert der häuslichen 230-V-Stromversorgung ist
	163 Volt.
	325 Volt.
	650 Volt.
	460 Volt.

Prüfungsfrage

TB610  Ein sinusförmiger Wechselstrom mit einer Amplitude (Imax) von 0,5 Ampere fließt durch einen Widerstand von 20 Ohm. Wie hoch ist die aufgenommene Leistung?
	0,5 W
	2,5 W
	5 W
	10 W

Lösung: Leistung ist immer ein Effektivwert. (Selbst wenn es die PEP-Leistung bei SSB ist, denn dort wird der Effektivwert einer Schwingung im Maximum der Modulationskurve berechnet.) Also müssen Sie zunächst den Effektivwert des Stromes berechnen, also geteilt durch Wurzel 2.

*)

Nun kann man damit die Spannung ausrechnen und dann U mal I rechnen oder direkt I² mal R.

Prüfungsfrage

TA114  Die Periodendauer von 50 µs entspricht einer Frequenz von
	200 Hz
	2 kHz
	20 kHz
	200 MHz

Lösung mit Hilfe der Formel für die Periodendauer

Für 10³ wurde kilo und für 1/s wurde Hz eingesetzt.

 

 

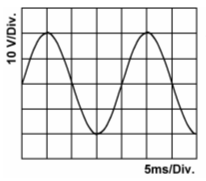
Signale auf dem Oszilloskop

Wechselspannungen werden normalerweise mit einem Oszilloskop dargestellt. Bei einem Oszilloskop findet man auf dem Schirmbild ein Raster, wobei man ein Kästchen als „Teilung“ (Division) bezeichnet.

Bild 11-2: Typisches Schirmbild eines Sinussignals

Es gibt zur Einstellung zwei Schalter am Oszilloskop (einen für vertikal, einen für horizontal), an denen der Wert des Rasters eingestellt werden kann. Man dreht an diesen Schaltern so lange bis man ein gut ablesbares Signal erhält. Dann multipliziert man die Spannungen mit dem Wert für ein Kästchen (Div).

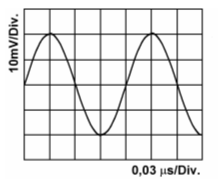
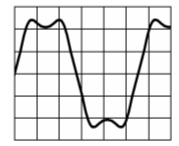
Prüfungsfrage

TB602  Wie groß ist der Spitzen-Spitzen-Wert (Uss) der in der Abbildung dargestellten Spannung?
	20 Volt
	40 Volt
	10 Volt
	4 Volt

Lösung: Zählen Sie die Kästchen (Div.) von der unteren Spitze bis zur oberen Spitze. Es sind vier Kästchen. Jedes Kästchen hat 10 V. Also ist der Spitze-Spitze-Wert 4 mal 10 V = 40 V.

Prüfungsfrage

TB603  Wie groß ist der Spitzen-Spitzen-Wert der in diesem Schirmbild dargestellten Spannung?
	12 Volt
	6 Volt
	8,5 Volt
	2 Volt

Prüfungsfrage

TB604  Welche Frequenz hat die in diesem Oszillogramm dargestellte Spannung?
	833,3 kHz
	83,3 kHz
	8,3 MHz
	83,3 MHz

Lösung: Zählen Sie die Anzahl der Kästchen horizontal für eine komplette Schwingung. Sie kommen hier auf vier Teilungen (Div.). Jedes Kästchen hat 3 Mikrosekunden, also sind es vier mal drei gleich zwölf Mikrosekunden. Dies ist die Periodendauer.

Aus der Periodendauer berechnen wir die Frequenz mit der Formel

Prüfungsfrage

TB605  Welche Frequenz hat das in diesem Schirmbild dargestellte Signal?
	16,7 MHz
	833 kHz
	8,33 kHz
	8,33 MHz

Lösung machen?

Prüfungsfrage

TB606  Welche Frequenz hat die in diesem Oszillogramm dargestellte Spannung?
	100 Hz
	50 Hz
	500 Hz
	1000 Hz

Lösung machen?

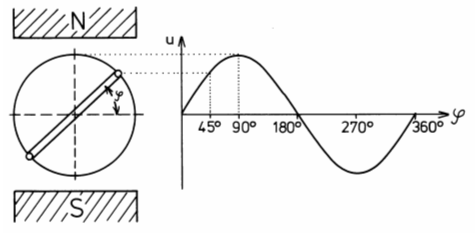
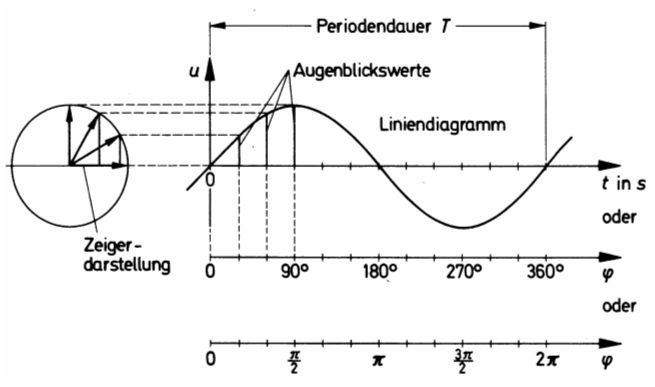
Ein sinusförmiges Signal entsteht beim Generator aus der Drehbewegung einer Spule. Der jeweilige Drehwinkel entspricht einer Spannung.

Bild 11-3: Erzeugung einer sinusförmigen Wechselspannung

Sie lernen jetzt, wie man eine sinusförmige Spannung durch Drehung eines Zeigers zeichnen kann. Aus dieser Konstruktion ergeben sich dann die Begriffe Kreisfrequenz und Phasenwinkel.

Die Werte im Liniendiagramm nennt man Augenblickswerte. Das sind die Werte, bei denen wir uns vorgestellt haben, dass der Zeiger einen Augenblick stoppt. Die zugehörigen Winkel im Zeigerdiagramm nennt man Phasenwinkel.

Bild 11-4: Die Zeigerdarstellung

 

Übungsaufgabe Zeichnen Sie selbst solch ein Liniendiagramm in das folgende Bild ein. Zeichnen Sie selbst die restlichen Pfeile über 90 Grad alle 30 Grad in den Kreis ein. Nun sollen Sie Werte aus dem Zeigerdiagramm in das Liniendiagramm übertragen. Nehmen Sie an, der Zeiger stoppt bei 30°. Die Höhe, die die Zeigerspitze von der Nulllinie hat soll nach rechts in das Liniendiagramm übertragen werden und zwar genau an die 30° Linie. Zeichen Sie dort einen Punkt ein. Gleiches machen Sie für 60°, für 90° und dann immer weiter, bis Sie wieder bei 0° ankommen. Verbinden Sie alle Punkte in dem Liniendiagramm. Sie müssten eine Sinuslinie bekommen wie im Bild 11-4.

Nehmen wir mal an, dass der Zeiger sich in einer Sekunde genau einmal komplett gedreht hat. Dann könnte man bei 360° auch 1 s dran schreiben und bei jedem Kästchen 1/36 davon. Das sind 0,02777 s pro Kästchen. Das ist zwar ein ungünstiger Maßstab, aber es funktioniert. Die horizontale Achse ist also gleichzeitig Winkelanzeige wie auch Zeitachse.

Aufgabe Lesen Sie einmal den Augenblickswert bei 45° ab, wobei der Radius den Wert „1“ haben soll. Haben Sie 0,7? Dies ist ein wichtiger Wert in der Elektrotechnik. Es ist dies der Wert "1 durch Wurzel 2", also 0,707. Berechnen Sie mit Ihrem Taschenrechner einmal den Wert sin(45°)!

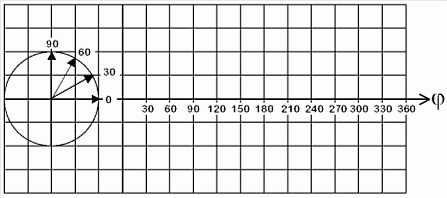
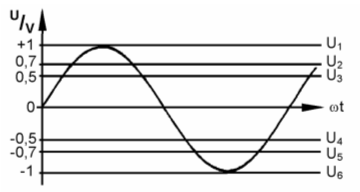
Lösung: sin(45°) = 0,707

 Noch etwas kommt in der Mathematik in diesem Zusammenhang häufig vor. Es ist das Bogenmaß. Man denkt sich den Kreis mit einem Radius von „1“. Das kann beispielsweise 1 m sein. Dann rechnet man den Umfang (Bogen) des Kreises aus. Der Umfang wird berechnet mit folgender Formel.

Bei r = 1 m wären es 2π Meter. Wenn man sich nicht auf Meter festlegt, sondern einfach sagt „Eine Längeneinheit“, dann ist der Umfang „2 π Längeneinheiten“ oder einfach 2 π im so genannten Einheitskreis. Dann kann man an die Achse im Liniendiagramm für einen Vollkreis (360°) auch einfach 2 π dran schreiben, wie im Bild 11-4 gezeigt. Genau der Hälfte, also 180° entspricht dann π und davon der Hälfte (90°) entsprechen π/2 und so weiter. Sie finden auch diese Skala im Bild 11-4. Passen Sie gut auf bei diesem Thema, denn dazu gibt es eine Prüfungsfrage. Schauen Sie noch einmal auf Bild 11-4 und vergleichen Sie folgende Gegenüberstellung.

π = 180°,       π/2 = 90°,         3 π/2 = 270°

Hinweis: Hier auf der Seite ist π (Schrift Verdana) = π (Schrift Times)

Prüfungsfrage

TB611  Welche Antwort enthält die richtigen Phasenwinkel einer sinusförmigen Wechselspannung an der im folgenden Bild mit X3 gekennzeichneten Stelle?
	π/3; 270°
	3π/4; 135°
	3π; 180°
	3π/2; 270°

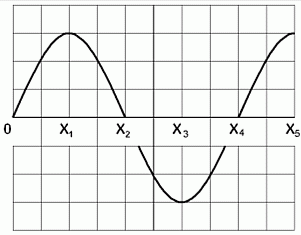
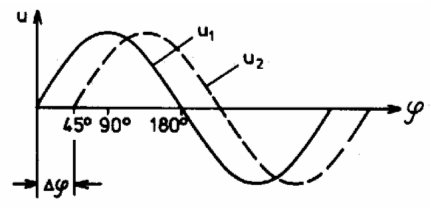
Lösung: Eine volle Schwingung hat 360 Grad. Diese Schwingung ist in vier Teile geteilt, also hat jeder Teil 90 Grad. Drei mal 90 gleich 270. Ferner entspricht einer vollen Schwingung das Bogenmaß 2 π, einem Viertel davon bei X₁ also 2 ^π/₄ = ^π/₂ und bei X₃ dreimal so viel, also 3 ^π/₂ oder 270°.

Wenn sich gleichzeitig mehrere in der Anordnung versetzte Spulen in einem Magnetfeld drehen und als Generatoren arbeiten, sind die Spannungen gegeneinander phasenverschoben, wie beispielsweise in folgendem Bild.

Bild 11-6: Phasenverschobene Spannungen

Man sagt, die Spannung u₂ eilt der Spannung u₁ um 45 Grad nach oder die Phasenverschiebung beträgt Δφ = 45°. Man schreibt gelegentlich kleine Buchstaben (u), wenn man damit andeuten möchte, dass es sich um Wechselspannungen handelt.

Prüfungsfrage

TB612  Die Phasendifferenz zwischen den beiden in folgender Abbildung dargestellten Sinussignalen beträgt
	0°
	45°
	90°
	180°

Lösung: Wenn man eine Sinuslinie verfolgt sieht man, dass eine Schwingung (360°) in acht Abschnitte geteilt ist. Ein Teilstrich sind dann 360 geteilt durch 8 gleich 45 Grad. Man sieht dann, dass beide Kurven um einen Teilstrich differieren.

Nur ein sinusförmiges Signal hat eine einzige Frequenz. Oder umgekehrt ausgedrückt. Hat ein Signal nur eine einzige Frequenz, ist es ein sinusförmiges Signal. Alle anderen Signale sind nichtsinusförmige Signale. Sie bestehen aus einem Frequenzgemisch.

Periodische Signale sind solche, die sich regelmäßig in gleicher Form wiederholen. Dazu gehören Rechtecksignale, Dreiecksignale, sägezahnförmige Signale und so weiter.

Diese periodischen Signale bestehen immer aus einer Grundfrequenz und ganzzahligen Vielfachen dieser Frequenz, die man Oberwellen oder Harmonische nennt. Die erste Oberwelle ist genau die doppelte Frequenz, die zweite Oberwelle ist die dreifache Frequenz und so weiter.

Bei der Zählweise der Harmonischen geht man von der Grundwelle aus. Die erste Harmonische ist die Grundwelle, die zweite Harmonische ist die zweifache Frequenz der Grundwelle und so weiter. Diese Zählweise ist international (harmonics). Mit Oberwellen rechnet man nur in Deutschland. Sie ist natürlich auch logischer, da man aus der Angabe direkt den Wert der Vielfachen erkennt, also z.B. ist die 4. Harmonische die vierfache Frequenz der Grundwelle.

Prüfungsfrage

TB703  Was sind Harmonische?
	Harmonische sind die ganzzahligen (1, 2, 3 ...) Vielfachen einer Frequenz.
	Harmonische sind die ganzzahligen (1, 2, 3 ...) Teile einer Frequenz.
	Harmonische sind die erzeugten Frequenzen oberhalb der ursprünglichen Frequenz.
	Harmonische sind identisch mit den Oberwellen, wobei die Grundwelle keine Harmonische ist.

Prüfungsfrage

TA115  Die zweite Harmonische der Frequenz 3,730 MHz befindet sich auf
	1,865 MHz.
	7,460 MHz.
	11,190 MHz.
	14,920 MHz.

Prüfungsfrage

TA116  Die zweite ungeradzahlige Harmonische der Frequenz 144,690 MHz ist
	145,000 MHz
	289,380 MHz
	434,070 MHz
	723,450 MHz

Lösung: Die erste Harmonische ist die Grundwelle, die zweite ist gerade und die dritte Harmonische (ungerade Zahl) ist die dreifache Frequenz.

Prüfungsfrage

TB704  Die dritte Oberwelle einer Frequenz ist
	die vierte Harmonische der Frequenz.
	die dritte Harmonische der Frequenz.
	die zweite Harmonische der Frequenz.
	die zweite ungeradzahlige Harmonische der Frequenz.

Prüfungsfrage

TF432  Auf welche Frequenz müsste ein Empfänger eingestellt werden, um die dritte Harmonische einer nahen 7,050-MHz-Aussendung erkennen zu können?
	21,15 MHz
	14,050 MHz
	24,15 MHz
	28,050 MHz

Prüfungsfrage

TF433  Auf welche Frequenz müsste ein Empfänger eingestellt werden, um die dritte Oberwelle einer 7,20-MHz-Aussendung erkennen zu können?
	28,80 MHz
	21,60 MHz
	24,20 MHz
	28,20 MHz

Tipp: Dritte Oberwelle ist vierfache Harmonische.

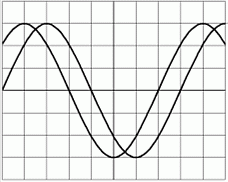
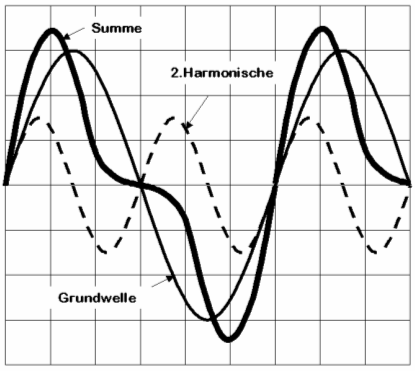
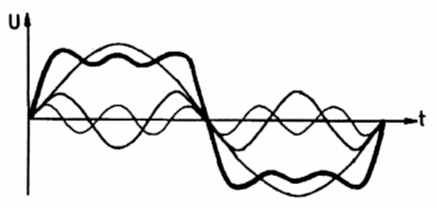
An zwei Beispielen soll gezeigt werden, wie durch Addition von reinen sinusförmigen Spannungen aus der Grundwelle und deren Harmonischen andere Schwingungsformen entstehen.

Bild 11-7: Entstehung einer Sägezahnschwingung durch Addition von Grundwelle und zweiter Harmonischen

Aufgabe Versuchen Sie es nachzuvollziehen. Zeichnen Sie auf kariertem Papier eine sinusähnliche Schwingung. Zeichnen Sie dort hinein eine weitere Sinusschwingung mit genau der doppelten Frequenz und der halben Amplitude. Bestimmen Sie bei jedem senkrechten Strich die Höhe der Amplituden beider Signale, indem Sie die Kästchen zählen. Addieren Sie die Werte anschließend (Beachten Sie die Vorzeichen!) und zeichnen Sie Punkte für die Summenspannungen ein. Verbinden Sie die Punkte miteinander. Sie müssten eine Skizze erhalten, die ähnlich dem obigen Bild aussieht.

Wenn Sie dann noch die dreifache Frequenz mit einem Drittel der Amplitude hinzunehmen, sehen Sie schon besser, dass der Anstieg der Kurve im positiven Bereich immer steiler wird und die hintere Flanke flacher. Es wird daraus eine Sägezahnspannung.

Bild 11-8: Sägezahnspannung

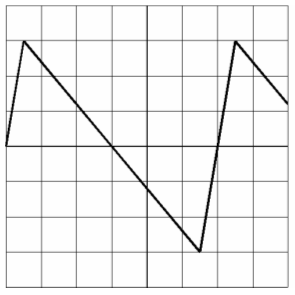
Also: Eine Sägezahnspannung enthält außer der Grundfrequenz alle ganzzahligen Vielfachen, also alle Harmonischen.

Prüfungsfrage

TB705  Welche Schwingungen sind in der folgenden Wechselspannung enthalten, wenn die Grundwelle 2 kHz beträgt?
	4 kHz und 6 kHz
	2 kHz und 6 kHz
	4 kHz allein
	2 kHz und 4 kHz

Tipp: Schauen Sie nocheinmal auf Bild 11-7!

Prüfungsfrage

TD414  Das folgende Oszillogramm zeigt die Ausgangsspannung eines Verstärkers, an dessen Eingang eine rein sinusförmige Wechselspannung anliegt. Welche Oberwelle wird von dem Verstärker erzeugt?
	Die zweite Harmonische
	Die dritte Harmonische
	Die vierte Harmonische
	Die fünfte Harmonische

Tipp: Die zweite Harmonische entspricht der doppelten Frequenz, denn die erste Harmonische ist die Grundwelle selbst.

Bild 11-9: Ein Rechtecksignal entsteht aus der Summe von ungeradzahligen Harmonischen.

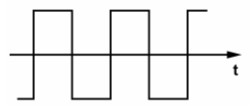
Zur Lösung der folgenden Aufgabe muss man wissen, dass Rechteckschwingungen außer der Grundwelle nur ungeradzahlige Vielfache enthalten. Gleiches gilt auch für Dreieckschwingungen. Das Rechtecksignal taucht in der Nachrichtentechnik sehr häufig auf, nämlich als digitales Übertragungssignal oder auch bei Übersteuerungen des Senders. Ein Funkamateur sollte wissen, dass diese Harmonischen Störungen verursachen können.

Prüfungsfrage

TB701  Ein symmetrisches Rechtecksignal hat eine Grundfrequenz von 1500 Hz. Welche Frequenzen sind in diesem Signal enthalten?
	1500 Hz, 3000 Hz, 4500 Hz und höher
	1500 Hz, 2250 Hz, 3000 Hz und höher
	1500 Hz, 4500 Hz, 7500 Hz und höher
	1500 Hz, 3000 Hz, 6000 Hz und höher

Tipp: Ungeradzahlige Vielfache sind die dreifache, die fünffache Frequenz und so weiter.

Prüfungsfrage

TB706  Welche Schwingungen sind in der folgenden Wechselspannung enthalten, wenn die Grundwelle 2 kHz beträgt?
	4 kHz und 6 kHz
	2 kHz und 4 kHz
	2 kHz und 6 kHz
	4 kHz allein

Prüfungsfrage

TD415  Das folgende Oszillogramm zeigt die Ausgangsspannung eines Verstärkers, an dessen Eingang eine rein sinusförmige Wechselspannung anliegt. Welche Oberwelle wird von dem Verstärker erzeugt?
	Die zweite Harmonische
	Die dritte Harmonische
	Die vierte Harmonische
	Die fünfte Harmonische

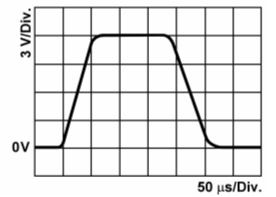
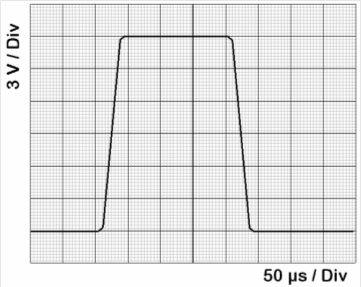
Tipp: Versuchen Sie der überlagerten Kurve zu folgen und zählen Sie, wie oft Sie eine komplette Schwingung durchfahren.

Bisher haben wir Signale kennen gelernt, die sich in der Form unterscheiden, also sinusförmiges Signal, Rechtecksignal, Dreiecksignal und so weiter. Wir haben sie unterteilt in sinusförmiges Signal und nichtsinusförmige Signale. Die Form dieser Signale ist periodisch wiederkehrend. Man kann eine Frequenz definieren, nämlich die Zeit, bei der sich der Vorgang (die Form) wiederholt. Man nennt sie auch periodische Signale. Es gibt Signale, die sich nicht regelmäßig wiederholen. Man nennt sie nicht-periodische Signale.

Zu den nicht-periodischen Signalen gehören die Impulse. Impulse sind einzeln oder in Gruppen auftretende Signale. Außer der Höhe der Impulse (Amplitude) ist die Impulsdauer ein wichtiger Kennwert. Die Impulsdauer ist definiert als die Zeit bei der die Anstiegsflanke 50 Prozent der Amplitude erreicht hat bis zu 50 Prozent der Amplitude der abfallenden Flanke.

Prüfungsfrage

TB702  Die Impulsdauer des Signals in folgendem Schirmbild beträgt
	160µs.
	12 V.
	260 µs.
	0,2 ms.

Lösung: Ziehen Sie in halber Höhe, also bei zwei Kästchen, einen waagerechten Strich. Zählen Sie die Anzahl der Kästchen auf der gezeichneten Linie. Sie sollten auf genau vier Kästchen kommen. Vier mal 50 µs sind 200 µs oder 0,2 ms.

Zeichnung für eine Ableseübung

 

Prüfungsfrage

TJ829  Die Pulsbreite wird mit einem Oszilloskop normalerweise bei
	90 % der Amplitude gemessen.
	50 % der Amplitude gemessen.
	70 % der Amplitude gemessen.
	10 % der Amplitude gemessen.

Modulierte Signale bestehen aus der Kombination von einem sinusförmigen Signal und weiteren sinusförmigen oder nicht-sinusförmigen Signalen oder Impulsen. Es ist keine Kombination (Addition) von Harmonischen, wie bei den nicht-sinusförmigen Signalen, sondern eine „Kombination“ von weit auseinander liegenden Frequenzen. Diese Kombination ist mathematisch betrachtet eine Multiplikation. Wir werden in dieser Lektion die mathematischen Zusammenhänge der Modulationsarten kennen lernen und in der folgenden Lektion die praktische Realisierung: Modulation und Demodulation.

Modulationsarten

Sie werden folgende Modulationsarten unterscheiden lernen.

Bild 11-11: Übersicht Modulationsarten

Um Signale von einem Ort zu einem anderen zu übertragen, bedient man sich der Hochfrequenztechnik. Es wird ein hochfrequenter Träger erzeugt, der von einer Antenne abgestrahlt und an einem anderen Ort (weltweit) von einer Antenne aufgefangen werden kann. Das Eigentliche Informationssignal wird dazu diesem "Träger" aufgeprägt. Dies nennt man Modulation.

Prüfungsfrage

TE104 Durch Modulation
	werden einem Träger Informationen entnommen.
	werden Informationen auf einen Träger aufgeprägt.
	werden Sprach- und CW-Signale kombiniert.
	werden dem Signal NF-Komponenten entnommen.

Eine hochfrequente Wechselspannung kann man mathematisch durch folgenden Ausdruck beschreiben.

Darin bedeutet u der Augenblickswert einer Wechselspannung in Abhängigkeit von der Zeit, û die Amplitude dieser Spannung, ω = 2 π  f die Kreisfrequenz und φ die Phasenlage dieser sinusförmigen Schwingung.

Man kann nun mit Hilfe der Modulation drei Größen dieser Schwingung in Abhängigkeit von der zeit beeinflussen. Verändert man die Amplitude û im Rhythmus des zu übertragenden Signals, erhält man Amplitudenmodulation (AM). Verändert man die Frequenz ω = 2 π  f  , erhält man Frequenzmodulation (FM). Verändert man φ, erhält man Phasenmodulation. Frequenzmodulation und Phasenmodulation zusammen nennt man Winkelmodulation. Die Phasenmodulation ist mit der Frequenzmodulation verwandt. Ändert man von einer Schwingung geringfügig die Frequenz, sieht es im Zeitdiagramm so aus, als hätte sich die Phase geändert.

Bild 11-10: Gegenüberstellung AM- FM-Signal

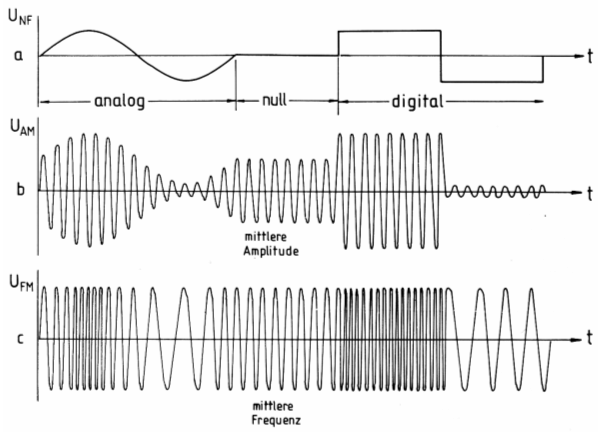
Bild 11-10a stellt das zu übertragende Informationssignal (NF) dar. Entsprechend der Modulationsspannung ändert sich die Amplitude bei AM (Bild b). Einer positiven Spannung entspricht eine große Amplitude der HF-Spannung und eine negative Signalspannung entspricht einer geringen Amplitude der Hochfrequenz. NF-Signalspannung Null entspricht dem Mittelwert.

Bei Frequenzmodulation (FM) bleibt die Amplitude immer gleich, nur die Anzahl der Schwingungen pro Zeiteinheit (die Frequenz) ändert sich. Und zwar entspricht hier eine positive NF-Spannung einer hohen Frequenz, eine negative NF-Spannung einer niedrigen Frequenz und keine NF-Spannung (Null) der mittleren Frequenz der hochfrequenten Trägerfrequenz.

Bei analoger Signalübertragung folgt die modulierte Spannung genau dem NF-Signal. Es gibt jeden Wert zwischen Null und dem Maximalwert. Bei digitaler Signalübertragung gibt es nur eine beschränkte Zahl von Werten (quantisiert) oder sogar nur zwei Werte (niedrig - hoch, null - eins) bei sogenannten binären Signalen. Dementsprechend ist bei binärer Informationsübertragung bei AM die Amplitude groß oder klein (eventuell null) oder bei FM die Frequenz hoch oder niedrig.

Zunächst soll geklärt werden, was Modulation technisch ist. Es ist eine mehr mathematische Betrachtung. In der folgenden Lektion folgt die technische Realisierung. Ich will Ihnen anhand einer kleinen mathematischen Betrachtung und dann unter Zuhilfenahme von gezeichneten Sinuskurven zeigen, dass Amplitudenmodulation immer eine Multiplikation von Signalen enthält. Die reine Multiplikation führt zu einem DSB-Signal. Die Addition plus Multiplikation führt zu normaler Amplitudenmodulation (AM). Bei Frequenzmodulation haben wir es mathematisch mit einem Sinus von einem Sinus zu tun. Dies führt zu einer Besselfunktion.

Mathematisch weniger Vorgebildete sollten vielleicht diesen Abschnitt mit dem „Mut zur Lücke“ überspringen. Viele Prüfungsaufgaben zu diesem Themenbereich gibt es nicht.

Bild 11-12: Addition und Multiplikation von zwei Frequenzen

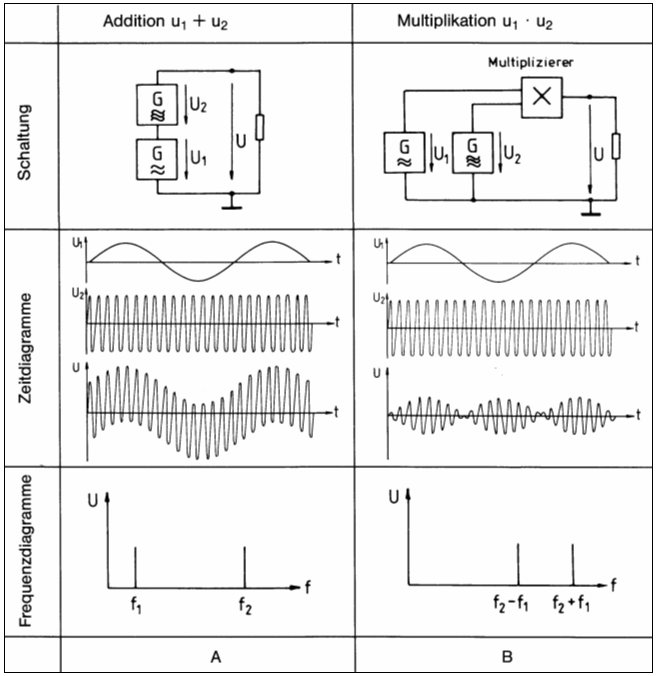
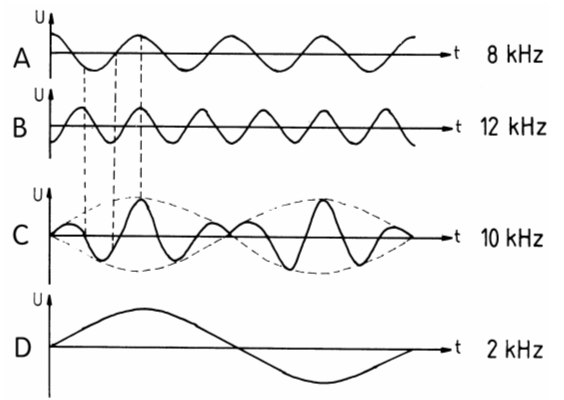
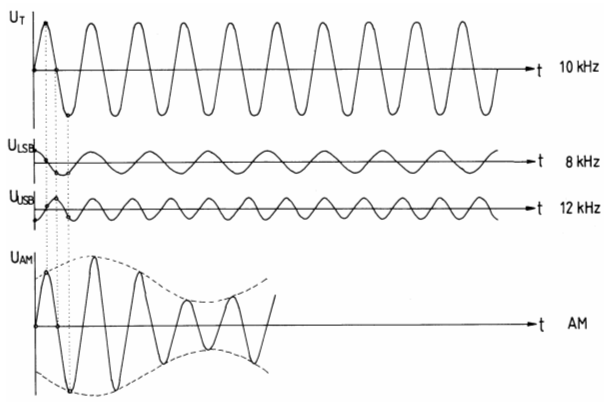
Betrachten wir das Bild 11-12. Es soll der Unterschied zwischen Addition von zwei Spannungen und Multiplikation deutlich gemacht werden. Addiert man in der Zeile „Zeitdiagramme“ punktweise zu jedem Augenblick die dargestellten Spannungen U₁ und U₂, erhält man die schlangenlinienartig verlaufende Spannung U, die man als Überlagerung bezeichnet. Dies ist noch keine Amplitudenmodulation, denn die Amplitude ist zu jedem Augenblick gleich groß. Die HF ist nur ein wenig nach oben und nach unten verschoben.

In der Spalte „Multiplikation“ sollen diese beiden Spannungen echt multipliziert werden. Dort, wo ein Signal null ist, ist natürlich auch das Produkt null. Wenn wir jetzt dieses neue Signal mit dem Summensignal vergleichen, haben wir wirklich eine Amplitudenänderung.

Wenn man das Signal U nach den darin enthaltenen Frequenzen untersucht (Spektrumanalysator) erkennt man unter Frequenzdiagramme in Bild 11-12 deutlich den Unterschied. Bei der Überlagerung (Addition) bleiben die beiden Frequenzen erhalten, während bei der Modulation (Multiplikation) zwei neue Frequenzen entstanden sind, nämlich die Summe und die Differenz der Frequenzen.

Ein kleiner Exkurs in die Mathematik soll dies ein wenig verdeutlichen. Bei der Summe von zwei sinusförmigen Signalen kann man folgenden Ausdruck schreiben.

Vereinfachen kann man diese Formel nicht mehr. Beide Frequenzen f₁ (als ω₁) und f₂ (als ω₂) sind erhalten geblieben. Anders ist es bei der Multiplikation.

Das Produkt Sinus mal Sinus kann man umrechnen. In der Mathematik gibt es dafür eine Formel.

Setzt man für α = ω₁·t  und für β = ω₂·t  ein, erhält man folgendes Ergebnis.

In den beiden Klammern stecken jeweils einmal die Summe und zum anderen die Differenz der beiden Frequenzen. Moduliert man beispielsweise einen Träger von 3700 kHz mit einem NF-Signal von 1 kHz, entstehen nur die Seitenfrequenzen von 3699 kHz und 3701 kHz. Solch ein Signal bezeichnet man auch als ein Doppelseitenband-Signal DSB mit Trägerunterdrückung.

Damit Sie nicht nur auf diese mathematische Erklärung angewiesen sind, will ich Ihnen mit einem Beispiel anhand von Sinuslinien zeigen, dass die Summe dieser beiden Seitenfrequenzen ein DSB-Signal ergibt. Ich wähle zur Demonstration zwei sehr niedrige Frequenzen. Angenommen, der Träger hat eine Frequenz von 10 kHz und dieser wird mit 2 kHz DSB-moduliert. Es entstehen die beiden Frequenzen 8 kHz (10-2) und 12 kHz (10+2).

Bild 11-13: Zweiseitenbandmodulation (DSB) mit unterdrücktem Träger

Im Bild 11-13 wurden zwei Kosinussignale A und B gezeichnet. Man muss an die Formel denken mit ein halb Kosinus ... minus ... Ich habe einmal 4 Schwingungen für 8 kHz und einmal 6 Schwingungen für 12 kHz gezeichnet. Dann habe ich punktweise addiert (gestrichelte Linien). Es entsteht ein DSB-Signal (C) mit 5 Schwingungen, also 10 kHz. Die Hüllkurve hat nur eine Schwingung, entsprechend 2 kHz. Mit anderen Worten: Ein DSB-Signal mit einer Hüllkurve von 2 kHz und einer Trägerfrequenz von 10 kHz ist dasselbe wie zwei halb so große Kosinussignale mit 8 kHz und 12 kHz.

Setzt man dem DSB-Signal noch die Trägerfrequenz selbst hinzu, entsteht ein AM-Signal. Dies zeige ich Ihnen wiederum durch die Addition von Träger- plus Seitenschwingungen anhand von Kosinuskurven niedriger Frequenz in folgendem Bild.

Bild 11-14: Entstehung von AM durch Addition von Träger- und Seitenschwingungen

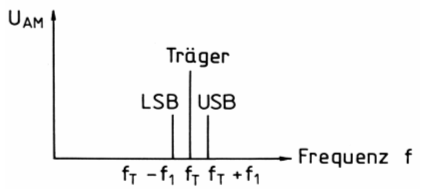
Zur Trägerfrequenz von 10 kHz (diesmal 10 Schwingungen) zeichne ich ein Viertel so große Kosinusschwingungen von 8 kHz und 12 kHz. Ich addiere diese drei Spannungen punktweise. Es entsteht ein Signal, dessen Amplitude sich gegenüber einem Mittelwert etwas erhöht und etwas erniedrigt (Bild 11-14 unten).

Daraus lässt sich umgekehrt folgendes schließen. Eine amplitudenmodulierte Schwingung lässt sich in eine Trägerschwingung sowie zwei weitere Schwingungen aus der Summe und der Differenz zerlegen. Die niedrigere Frequenz (Differenz) nennt man untere Seitenschwingung, die höhere Frequenz obere Seitenschwingung.

Bild 11-15: Spektrum eines AM-Signals, das mit einer einzelnen Frequenz moduliert ist

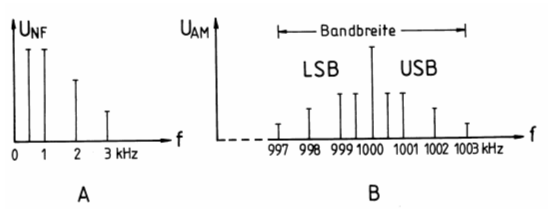
Bei der Übertragung von Sprache besteht das Informationssignal (NF) nicht nur aus einer einzigen Frequenz, sondern aus einem Frequenzgemisch. Wenn ein bestimmter Laut gesprochen wird, soll das Informationssignal beispielsweise aus den Frequenzanteilen 0,5 kHz, 1 kHz, 2 kHz mit unterschiedlichen Lautstärken (Amplituden) bestehen (Bild 11-16A). Wird der Träger mit diesem Frequenzband moduliert, ergeben sich auch wieder die Summen und die Differenzen und es entsteht ein Spektrum nach Bild 11-16B.

Bild 11-16: A: NF-Frequenzspektrum
B: Spektrum der Zweiseitenband-AM

Die entstehenden Seitenfrequenzen nennt man Seitenbänder und unterscheidet LSB (lower side band) und USB (upper side band). Das Ganze ist analoge Zweiseitenbandmodulation mit Träger, international als Sendeart mit A3E abgekürzt, wenn das Informationssignal Sprache ist.

Prüfungsfrage

TB802  Ein Träger von 7,05 MHz wird mit der NF-Frequenz von 2 kHz in SSB (LSB) moduliert. Welche Frequenzen treten im modulierten HF-Signal auf?
	7,048 MHz
	7,050 MHz
	7,052 MHz
	7,048 MHz und 7,052 MHz

Bandbreite bei DSB

Die Bandbreite ist der Unterschied von der niedrigsten bis zur höchsten vorkommenden Frequenz. Wie aus Bild 11-16 B zu erkennen ist, geht die Bandbreite von 997 bis 1003 kHz, beträgt also 6 kHz. Man kann die Bandbreite für AM auch mit folgender Formel ausrechnen:

b_AM = 2 · f_mod

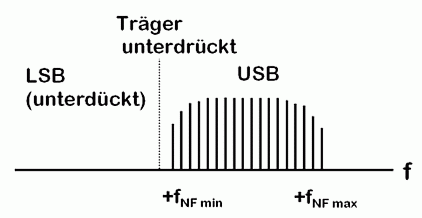
Die Bandbreite bei Zweiseitenband-AM ist doppelt so groß wie die höchste vorkommende Modulationsfrequenz.

Um Bandbreite zu sparen gibt es die Möglichkeit, eines der beiden Seitenbänder von DSB wegzufiltern und nur eines durchzulassen. Diese Modulationsart heißt dann SSB (single side band) oder international J3E.

Bild 11-17: Spektrum bei USB -
Einseitenbandmodulation mit unterdrücktem Träger

Lässt man das untere Seitenband durch, heißt die Modulationsart in der Abkürzung LSB (lower side band). Lässt man das obere Seitenband durch, erhält man USB (upper side band). Eigentlich ist es egal, welches Seitenband man verwendet. Beide Seitenbänder führen die gleiche Information. Im Amateurfunk hat es sich „eingebürgert“, dass man bei Frequenzen unterhalb 10 MHz das untere Seitenband und oberhalb 10 MHz das obere Seitenband verwendet. Es hat historische Gründe bei der Erzeugung von SSB und der Verwendung nur eines einzigen Filters.

Die Bandbreite bei SSB ergibt sich aus der Differenz der höchsten und der niedrigsten Modulationsfrequenz.

Weil die niedrigste Frequenz NF_min normalerweise gegenüber NF_max sehr gering ist, kann man diese vernachlässigen und schreibt

Gegenüber AM wird die Bandbreite praktisch halbiert und es können doppelt so viele Sender in einem Frequenzband arbeiten.

Prüfungsfrage

TB801  Wie groß ist die HF-Bandbreite, die für die Übertragung eines SSB-Signals erforderlich ist?
	Sie entspricht der Hälfte der Bandbreite des NF-Signals.
	Sie entspricht genau der Bandbreite des NF-Signals.
	Sie entspricht der doppelten Bandbreite des NF-Signals.
	Sie ist Null, weil bei SSB-Modulation der HF-Träger unterdrückt wird.

Für die folgende Prüfungsaufgabe müssen Sie wissen, dass man international die Modulationsart Sprechfunk AM mit A3E und die Modulationsart Sprechfunk SSB mit J3E bezeichnet. Siehe hierzu die Tabelle am Schluss dieser Lektion.

Prüfungsfrage

TE101  Wie unterscheidet sich J3E von A3E in Bezug auf die benötigte Bandbreite?
	Die Sendeart J3E beansprucht etwas mehr als die halbe Bandbreite der Sendeart A3E.
	Die Sendeart J3E beansprucht etwa ¼ Bandbreite der Sendeart A3E.
	Die Sendeart J3E beansprucht weniger als die halbe Bandbreite der Sendeart A3E.
	Die unterschiedlichen Sendearten lassen keinen Vergleich zu, da sie grundverschieden erzeugt werden.

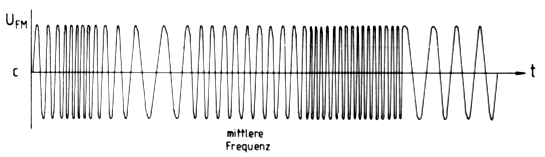
Es geht in dieser Lektion noch nicht um die Schaltungen der Modulationsarten sondern um die Signale selbst.

Die Modulationsspannung erzeugt bei FM die Frequenzänderung, wie sie in folgendem Bild dargestellt ist. Je größer die Lautstärke wird, desto höher wird die Modulationsamplitude und desto stärker wird die Trägerfrequenzauslenkung. Diese Trägerfrequenzauslenkung nennt man Frequenzhub oder kurz Hub Df.

Bild 11-18: Der Hub ist von der Lautstärke abhängig

Die Amplitude eines FM-Signals ändert sich dabei nicht.

Bild 11-19: FM-Signal

Im Amateurfunklehrgang Klasse E wurde bereits erklärt, dass wegen der immer gleich bleibenden Amplitude und der möglichen Amplitudenbegrenzung im Empfänger Impulsstörungen (Zündfunken von Fahrzeugen oder elektrostatische Entladungen bei Gewitter), die sich auf ein Funksignal auswirken können, abgeschnitten und damit fast unhörbar werden. Bei amplitudenmodulierten Signalen (dazu gehören außer AM auch SSB und CW) wirken sich diese Störungen sehr stark aus.

Prüfungsfrage

TE109  Welche Sendeverfahren weisen das größte Störpotential in Bezug auf NF-Verstärkersysteme auf?
	Frequenzmodulation (FM) und Frequenzumtastung (FSK).
	Einseitenbandmodulation (SSB) und Morsetelegrafie (CW).
	Frequenzumtastung (FSK) und Morsetelegrafie (CW).
	Einseitenbandmodulation (SSB) und Frequenzmodulation (FM).

Prüfungsfrage

TE201  Welche nachfolgende Sendeart hat die geringste Störanfälligkeit bei Funkanlagen in Kraftfahrzeugen?
	C3F*), weil hier die wichtige Information in der Amplitude des Restseitenbandes enthalten ist.
	J3E, weil hier die wichtige Information in der Amplitude eines Seitenbandes enthalten ist.
	F3E, weil hier die wichtige Information nicht in der Amplitude enthalten ist.
	A3E, weil hier die wichtige Information in den Amplituden der beiden Seitenbänder enthalten ist.

*) Die Abkürzungen finden Sie ganz unten auf dieser Seite.

Prüfungsfrage

TE206  FM hat gegenüber AM den Vorteil der
	geringen Anforderungen an die Bandbreite.
	geringeren Beeinflussung durch Störquellen.
	größeren Entfernungsüberbrückung.
	besseren Kreisgüte.

Prüfungsfrage

TF330  Der Begrenzerverstärker eines FM-Empfängers ist ein Verstärker,
	der das Ausgangssignal ab einem bestimmten Eingangspegel begrenzt.
	der zur Verringerung des Vorstufenrauschens dient.
	der zur Begrenzung des Hubes für den FM-Demodulator dient.
	der den ZF-Träger unabhängig vom Eingangssignal auf niedrigem Pegel konstant hält.

Modulationsindex bei FM

Im Amateurfunk wird ein typischer Frequenzhub Df_T von 3 bis 5 kHz verwendet (Schmalband-FM, NBFM), während man im UKW-Rundfunk 75 kHz (Breitband-FM, WBFM) verwendet.

Prüfungsfrage

TE217  Der typische Hub eines NBFM-Signals (Schmalband-FM) im Amateurfunk beträgt
	3 kHz.
	500 Hz.
	7,5 kHz.
	25 kHz.

Prüfungsfrage

TE204  Wodurch wird bei Frequenzmodulation die Lautstärke-Information übertragen?
	Durch die Geschwindigkeit der Trägerfrequenzänderung.
	Durch die Größe der Trägerfrequenzauslenkung.
	Durch die Änderung der Geschwindigkeit des Frequenzhubes.
	Durch die Größe der Amplitude des HF-Signals.

Prüfungsfrage

TK208  Parasitäre Schwingungen können Störungen hervorrufen. Man erkennt sie auch daran, dass sie
	bei ungeradzahligen Vielfachen der Betriebsfrequenz auftreten.
	bei ganzzahligen Vielfachen der Betriebsfrequenz auftreten.
	bei geradzahligen Vielfachen der Betriebsfrequenz auftreten.
	keinen festen Bezug zur Betriebsfrequenz haben.

Bei Frequenzmodulation gibt es drei wichtige Kennwerte und zwar außer dem Hub noch den Modulationsindex und die Bandbreite. Der Hub wurde bereits definiert. Der Modulationsindex ist das Verhältnis von Hub zu maximaler Modulationsfrequenz.

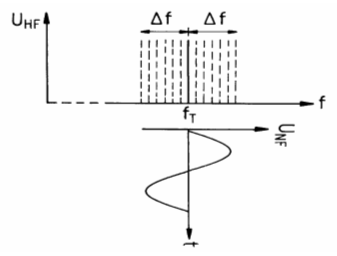
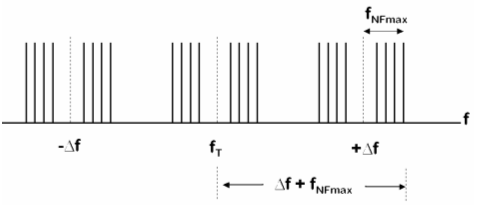
Im UKW-Rundfunk wird 75 kHz Hub verwendet bei einer höchsten Modulationsfrequenz von 15. Dies ergibt einen Modulationsindex von 5.

Theoretisch entstehen bei Frequenzmodulation eine unendliche Zahl von Seitenfrequenzen, die aber mit zunehmenden Abstand vom Träger je nach Hub schnell kleiner werden. Bei kleinem Modulationsindex kann man ein vereinfachtes Frequenzspektrum annehmen, bei dem nur Seitenfrequenzen bis 1 % der Trägerleistung berücksichtigt werden, das folgendermaßen aussieht.

Bild 11-20: Vereinfachtes Frequenzspektrum bei FM

Prüfungsfrage

TE205  Theoretisch arbeitet die Frequenzmodulation mit
	nur zwei Seitenbändern.
	nur einem Seitenband.
	keinen Seitenbändern.
	einer unendlichen Anzahl von Seitenfrequenzen.

Nach dem Bild beträgt die Bandbreite bei FM

Überschlagsmäßig könnte man die Bandbreite grob angeben als zweimal Hub. Das wären dann 150 kHz. Also wenn die Modulationsfrequenz klein ist gegenüber dem Hub gilt

Prüfungsfrage

TE203  Was gilt in etwa für die Bandbreite B eines FM-Signals, wenn der Modulationsindex m > 2 wird? (fmod sei die Modulationsfrequenz und Δf der Hub.)
	fmod < Δf.  Die Bandbreite wird im wesentlichen durch Δf bestimmt; B ≈ 2 · Δf .
	fmod > Δf.  Die Bandbreite wird im wesentlichen durch fmod bestimmt; B ≈ 2 · fmod .
	fmod > .  Die Bandbreite wird im wesentlichen durch m·Δf bestimmt; B ≈ 2 · fmod .
	fmod < Δf.  Die Bandbreite wird im wesentlichen durch m · fmod bestimmt; B ≈ 2 · fmod .

Frequenzmodulation mit einem Modulationsindex von kleiner als 0,5 (an anderer Stelle steht 1,0) nennt man Schmalband-Frequenzmodulation (NBFM). Dafür gilt folgende Bandbreitenberechnung.

also praktisch die gleiche Bandbreite wie bei AM.

Prüfungsfrage

TE202  Was gilt in etwa für die Bandbreite B eines FM-Signals, wenn der Modulationsindex m < 0,5 wird? (fmod sei die Modulationsfrequenz und Δf der Hub.)
	fmod < Δf.  Die Bandbreite wird im wesentlichen durch Δf bestimmt; B ≈ 2 · Δf .
	fmod > Δf.  Die Bandbreite wird im wesentlichen durch fmod bestimmt; B ≈ 2 · fmod .
	fmod > .  Die Bandbreite wird im wesentlichen durch m·Δf bestimmt; B ≈ 2 · fmod .
	fmod < Δf.  Die Bandbreite wird im wesentlichen durch m · fmod bestimmt; B ≈ 2 · fmod .

Prüfungsfrage

TB803  Ein Träger von 145 MHz wird mit der NF-Frequenz von 2 kHz und einem Hub von 1,8 kHz frequenzmoduliert. Welche Bandbreite hat das modulierte Signal?
	Die Bandbreite beträgt ungefähr 3,8 kHz
	Die Bandbreite beträgt ungefähr 7,6 kHz
	Die Bandbreite beträgt ungefähr 5,8 kHz
	Die Bandbreite beträgt ungefähr 12 kHz

Tipp zu TB803: Der Modulationsindex ist 1,8 geteilt durch 2, also kleiner als 1. Das zählt noch zu Schmalband-FM. Damit treten die gleichen Frequenzen auf wie bei AM, also Träger sowie Summe und Differenz.

Ein zu großer Hub erzeugt weitere Seitenfrequenzen, was zu Störungen in den Nachbarkanälen führen kann.

Prüfungsfrage

TE207  Ein zu großer Hub eines FM-Senders führt dazu,
	dass die HF-Bandbreite zu groß wird.
	dass die Sendeendstufe übersteuert wird.
	dass Verzerrungen auf Grund unerwünschter Unterdrückung der Trägerfrequenz auftreten.
	dass Verzerrungen auf Grund gegenseitiger Auslöschung der Seitenbänder auftreten.

Prüfungsfrage

TE210  Eine FM-Telefonie-Aussendung mit zu großem Hub führt möglicherweise
	zur Übersteuerung der Sendeendstufe.
	zu Nachbarkanalstörungen.
	zu Verzerrungen auf Grund unerwünschter Unterdrückung der Trägerfrequenz.
	zu Verzerrungen auf Grund gegenseitiger Auslöschung der Seitenbänder.

Prüfungsfrage

TE211  Was bewirkt die Erhöhung des Hubes eines frequenzmodulierten Senders?
	Eine größere Sprachkomprimierung.
	Eine geringere Störung der Nachbarkanäle.
	Eine stärkere Unterdrückung von FM-Geräuschen.
	Eine höhere HF-Bandbreite.

Prüfungsfrage

TE212  Größerer Frequenzhub führt bei einem FM-Sender zu
	einer Erhöhung der Senderausgangsleistung.
	einer größeren HF-Bandbreite.
	einer Erhöhung der Amplitude der Trägerfrequenz.
	einer Reduktion der Amplituden der Seitenbänder.

Zum Thema Frequenzmodulation finden sich im Fragenkatalog noch zwei Fragen zur Messung des Hubs mittels Spektrumanalysator. Die Theorie dazu ist sehr schwer zu erklären, denn bei Frequenzmodulation handelt es sich mathematisch um einen Sinus von einem Sinus, also sin(sin ωt + j). Diese Funktion zu beschreiben ist nur mit Hochschulwissen möglich und erfordert Kenntnisse über die „Besselfunktion“.

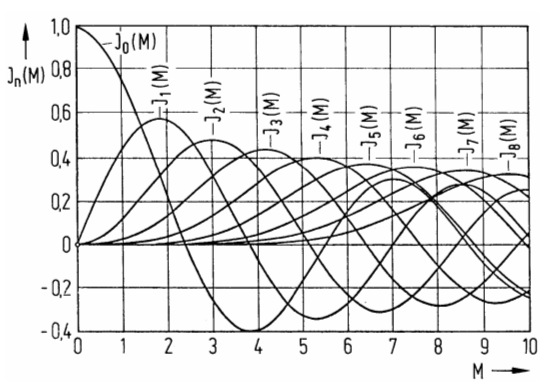
Für Interessierte habe ich nach der horizontalen Linie einen Exkurs zu diesem Thema gemacht. Sie können diesen Teil überspringen, wenn es Ihnen zu mathematisch erscheint. Nach der nächsten Linie geht es dann "normal" weiter.

Sie haben gemerkt, dass es bei der Bandbreitenberechnung für Frequenzmodulation sehr ungenaue „Ungefährformeln“ gibt, die dann entweder für einen sehr geringen oder einen großen Modulationsindex gelten sollen. Man kann die Bandbreite natürlich sehr genau berechnen. Dazu wird aber eine Funktion aus der höheren Mathematik gebraucht. Ich möchte nun denjenigen, die entsprechende Vorkenntnisse haben, diese Funktion etwas erläutern und an einem Beispiel vorführen, wie man die Bandbreite bei FM sehr genau berechnen kann.

Die mathematische Beschreibung für den zeitlichen Verlauf des FM-Signals lautet

Sie sehen: Es gibt eine Formel mit einem Sinus von einem Sinus. Die Ausrechnung der ineinander geschachtelten Winkelfunktionen ergibt eine Überlagerung von Sinuskurven, deren Amplituden vom Modulationsindex abhängen. Dies führt zur Besselfunktion J_n(M). Ich möchte Ihnen diese wahnsinnig lange Formelgleichung ersparen. Ich gebe Ihnen die Besselfunktion grafisch und erläutere, wie man damit die Bandbreite berechnet.

Bild 11-21: Die Bessel-Funktionen

Übungsbeispiel Es soll die Bandbreite für ein Amateurfunk FM-Signal berechnet werden. Gegeben: Höchste Frequenz 3 kHz, Hub 5 kHz.

Lösung: Zunächst wird M berechnet.

Bei M = 1,67 ziehe ich einen senkrechten Strich in der Besselfunktion. Dann lese ich für alle Seitenfrequenzen J₀, J₁, J₂ ... die Amplitudenwerte ab. J₀ bedeutet Trägerfrequenz, J₁ bedeutet erste Seitenfrequenz, also plus 3 kHz bei uns, J₂ bedeutet zweite Seitenfrequenz, also plus 3 kHz und so weiter.

f_T : J₀ = 0,5
f_T ± 3 kHz : J₁ = 0,55
f_T ± 6 kHz : J₂ = 0,3
f_T ± 9 kHz : J₃ = 0,1
f_T ± 12 kHz : J₄ < 0,05

Amplituden kleiner als 0,1 braucht man nicht mehr zu berücksichtigen. So genau kann man nicht ablesen in diesem Minidiagramm. Die höchste noch zu berücksichtigende Amplitude wäre J3. Daraus ergibt sich eine Bandbreite von zweimal 9 gleich 18 kHz. Mit der Ungefährformel erhielten wir

Damit liegen wir mit der Ungefährformel gar nicht so schlecht.

Übungsaufgabe Berechnen Sie die FM-Bandbreite für Df = 3 kHz und fmax = 3 kHz.

Lösung: M = 1. Ich schaue nur, bei welcher Besselfunktion J_n(M) der Wert größer ist als 0,1. J2 muss noch berücksichtigt werden. Also B wird zweimal 6 kHz gleich 12 kHz.

“Bessel” für alle

Merken: Aus der Besselfunktion erkennt man, dass bei einem Modulationsindex von 2,4 und von 5,5 und weiter bei 8,6 die Besselfunktion J₀ (Trägerfrequenz) eine Nullstelle erreicht. Man kann mit diesem Wissen eine Hubkontrolle mit einem Spektrumanalysator durchführen.

Prüfungsfrage

TE214  Am Spektrumanalysator zeigt ein FM-Sender bei der Modulation mit einem 1-kHz-Ton die erste Trägernullstelle. Wie groß ist der Spitzenhub?
	1,7 kHz
	2,4 kHz
	4,8 kHz
	3,4 kHz

Zur Frage TE214: Bei der ersten Nullstelle weiß man, dass der Modulationsindex 2,4 beträgt. Damit lässt sich der Hub berechnen.

Also merken Sie sich besonders für die Beantwortung dieser beiden Fragen diese Tatsache, dass bei einem Modulationsindex von 2,4 die Trägerfrequenz eine erste Nullstelle im Spektrum bekommt.

Auch die Prüfungsfrage TE215 kann man mit diesem Wissen beantworten.

Prüfungsfrage

TE215  Wenn ein FM-Sender mit einem Modulationsindex m = 2,4 betrieben wird,
	hat seine Trägerfrequenz eine Nullstelle.
	nimmt der Trägerpegel um den Faktor 2,4 zu.
	verändert sich der Trägerpegel nicht, da es sich um FM handelt.
	ist der maximale Hub erreicht.

Frequenzumtastung FSK

Die bei Funkfernschreiben übliche Frequenzumtastung gehört ebenfalls zu den frequenzmodulierten Signalen. Die RTTY-Signale werden bei FSK als Spannungswerte 0 und 5 Volt ausgegeben und damit im Sender der Oszillator auf zwei Frequenzen hin und her geschaltet.

Die Bandbreite bei FSK ergibt sich aus Hub plus höchster Umschaltfrequenz. Die höchste Umschaltfrequenz ist ungefähr die halbe Baudrate. Dazu mehr in der folgenden Lektion!

Modulation mit Hilfsträger

Anstatt die Information direkt auf den Träger aufzumodulieren, kann man einen niederfrequenten Zwischenträger mit der gewünschten Information modulieren und das entstandene Gesamtsignal dann in AM oder in FM auf den Hauptträger zu modulieren. Für einen Morselehrgang auf den 2-m-FM-Kanälen beispielsweise, tastet man ein 1-kHz-Tonsignal mit dem Morsecode. Dieses bereits getastete Signal gibt man dann auf den Mikrofoneingang des FM-Senders. Diese Sendeart bezeichnet man als Frequenzmodulation mit Tastung eines modulierten Hilfsträgers F2A gemäß Tabelle auf folgender Seite.

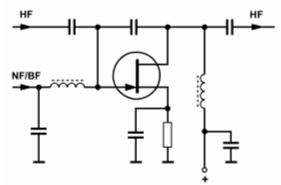
Phasenmoduliertes Signal

Heutzutage im Zeitalter der integrierten Bausteine und der Digitaltechnik erzeugt man Frequenzmodulation nicht mehr mit einem Oszillator und einem LC-Schwingkreis, sondern durch phasengesteuerte Schleifen in Zusammenarbeit mit spannungsgesteuerten Oszillatoren auf Quarzbasis. Damit lässt sich auch eine Modulation erreichen, die sich wie Frequenzmodulation auswirkt, aber eigentlich nur die Phase des Signals steuert.

Man kann auch einen Transistor als Phasenschieber schalten, indem man über einen Kondensator (90° Phasenverschiebung) eine Rückkopplung auf einen 180°-Verstärker (Emitterschaltung oder Sourceschaltung) einstellt. Solch eine Schaltung ist in folgender Prüfungsfrage dargestellt.

Prüfungsfrage

TD515  Bei dieser Schaltung handelt es sich um einen Modulator zur Erzeugung von
	phasenmodulierten Signalen.
	frequenzmodulierten Signalen.
	AM-Signalen mit unterdrücktem Träger.
	AM-Signalen.

Auf der Empfängerseite ist bei kleinem Phasenhub keine Unterscheidung zwischen FM und PM möglich. Diese PM-Sender werden deshalb auch als FM-Sender bezeichnet. Eine weitere Besprechung von Phasenmodulation erfolgt im Amateurfunklehrgang nicht, aber die PLL-Oszillatoren werden Sie noch kennen lernen.

Prüfungsfrage

TB805  Kann man auf der Empfängerseite bei Sprachübertragung Frequenz- und Phasenmodulation unterscheiden?
	Ja, weil bei Phasenmodulation die Frequenz immer konstant ist.
	Nein, im Normalfall ist keine Unterscheidung möglich.
	Ja, weil bei Frequenzmodulation ein kräftigeres Signal erzeugt wird.
	Ja, weil phasenmodulierte Aussendungen in FM-Empfängern bzw. frequenzmodulierte Aus­sendungen in Phasendiskriminatoren erhebliche Verzerrungen verursachen.

Internationale Kennzeichnung der Sendearten

 

1.Symbol: Modulationsart des Hauptträgers
A	Zweiseitenband AM
C	Restseitenband AM
F	Frequenzmodulation
G	Phasenmodulation
J	Einseitenband AM, unterdrückter Träger

 

2.Symbol: Signalmodulation des Hauptträgers
1	Einkanal mit quantisierter oder digitaler Information ohne Modulation des Hilfsträgers
2	Einkanal mit quantisierter oder digitaler Information mittels eines modulierten Hilfsträgers
3	Einkanal mit analoger Modulation

 

3.Symbol: Art der auszusendenden Information
A	Tastung durch Morsetelegrafie
B	Fernschreiben
C	Faksimile (Bildübertragung)
D	Datenübertragung, Fernsteuerung
E	Sprechfunk
F	Fernsehen (Video)

 

Beispiele J3E Sprechfunk (E) in Einseitenbandmodulation mit unterdrücktem Träger (J), analog. Das ist die Modulationsart, die wir im Amateurfunk mit SSB bezeichnen. A1A ist normale Morsetelegrafie (CW). Man tastet die Amplitude des Trägers (AM). F2B ist Funkfernschreiben (RTTY) mit Frequenzumtastung. C3F ist ATV Amateurfunkfernsehen (Restseitenbandverfahren)

Anhang

Dieser Online-Lehrgang wurde mit freundlicher Genehmigung des Autors aus seinem Buch für das Internet umgewandelt.

Eckart K. W. Moltrecht, "Amateurfunklehrgang für das Amateurfunkzeugnis Klasse 1+2 - TECHNIK" Verlag für Technik und Handwerk, Postfach 2274, 76492 Baden-Baden, 2. Auflage 2007, 309 Seiten, mehr als 300 Abb. ISBN 3-88180-389-0           17,80 €         online bestellen Die 3. Auflage (Klasse A) erscheint im April 2007 *)

Dieser Lehrgang basiert auf dem Prüfungsfragenkatalog Feb. 2007 der Bundesnetzagentur (BNetzA). Alle darin vorkommenden Themen wie Grundlagen der Elektrotechnik, Elektronik sowie Sender- und Empfängertechnik, Übertragungstechnik, Antennentechnik und Messtechnik aus dem Gebiet "Technische Kenntnisse" werden ausführlich erläutert. Die Erfahrung mit praktischen Lehrgängen wird genutzt, um den Prüfling in die Lage zu versetzen, jede Frage aus dem Fragenkatalog richtig zu beantworten. Dieses Buch ist auch sehr gut für das Selbststudium geeignet. Dieser Lehrgang baut auf dem Lehrgang für die Klasse E auf. Sie sollten also erst den Lehrgang für das Amateurfunkzeugnis Klasse E durchgearbeitet haben oder zumindest bei Verweisen dort nachlesen können.

*) Wenn Sie noch vor dem 1. Juni die Prüfung Klasse A (nach dem alten Fragenkatalog Klasse 1+2) machen wollen, sollten Sie sich dieses Buch besorgen, denn es wird in Kürze ausverkauft sein. Bis Ende Mai wird noch nach dem alten Fragenkatalog geprüft. Dieses Buch online bestellen

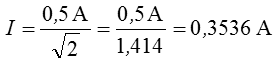Letztes Update: 18.3.2007 (by DJ4UF)