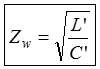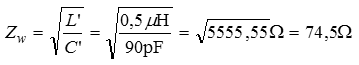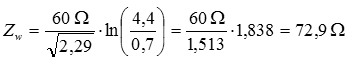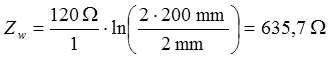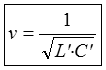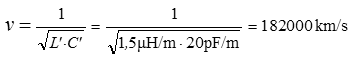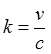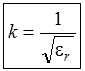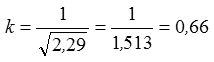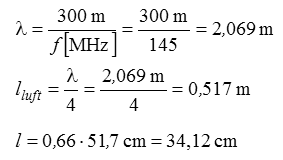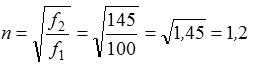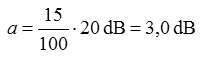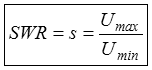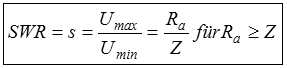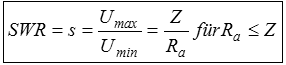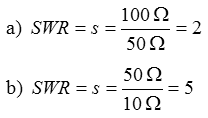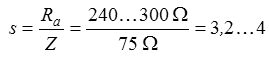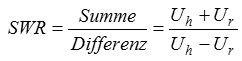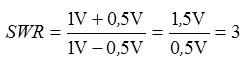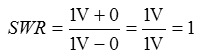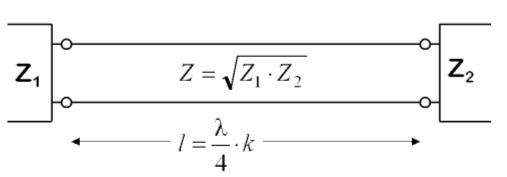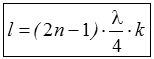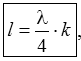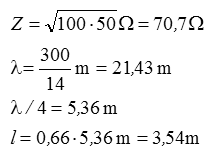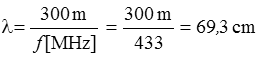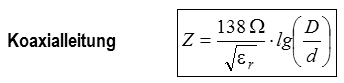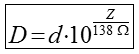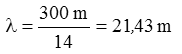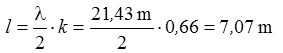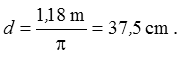Lehrgang nach dem neuen Fragenkatalog vom 28.2.2007

Hochfrequenzleitungen dienen dazu, entweder die vom Sender produzierte Hochfrequenzenergie zur Antenne zu führen oder umgekehrt, die von der Antenne aufgefangene HF-Energie zum Empfänger zu leiten. In der Sendertechnik soll die Hochfrequenzleistung möglichst ohne Verluste zur Antenne gelangen. Deshalb müssen verlustarme Leitungen verwendet werden.

Übersicht

• Der Wellenwiderstand
• Der Verkürzungsfaktor
• Die Dämpfung
• Das Stehwellenverhältnis
• Die Lecherleitung
• Transformationsleitungen
• Die Symmetrierung
• Der Topfkreis

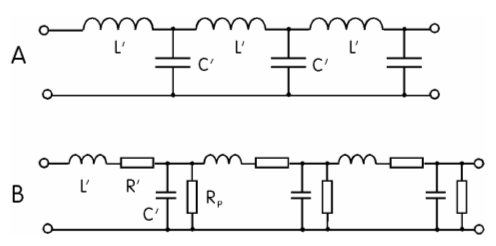
Der Wellenwiderstand

Eine Leitung besteht im Prinzip aus der Reihenschaltung vieler kleiner Induktivitäten und der Parallelschaltung vieler kleiner Kapazitäten (a). Berücksichtigt man noch den Leitungswiderstand R’ und den Isolationswiderstand R_P, erhält man das exakte Leitungsersatzbild (b).

Bild 10-1: a) Ersatzbild, b) exaktes Ersatzbild einer Leitung

Man nennt die Kapazität pro Meter Länge einer Leitung den Kapazitätsbelag C’ und die Induktivität pro Meter den Induktivitäts­belag L’. Aus diesen beiden Werten kann man einen wichtigen Kennwert einer Leitung berechnen, den Wellenwiderstand.

Beispiel
Von einem Meter Kabel wurde im Leerlauf die Kapazität von 90 pF und bei Kurzschluss die Induktivität von 0,5 µH gemessen. Wie groß ist der Wellenwiderstand dieser Leitung?

Lösung:

Der Wellenwiderstand ist unabhängig von der Länge der Leitung, denn verdoppelt man die Länge, erhält man doppelte Induktivität und doppelte Kapazität. Der Wellenwiderstand bleibt gleich. Er ist auch unabhängig von der Frequenz. Es kommt kein f in der Formel vor!

Prüfungsfrage

TH301  Der Wellenwiderstand einer Leitung
	ist völlig frequenzunabhängig.
	ist im HF-Bereich in etwa konstant.
	hängt von der Beschaltung am Leitungsende ab.
	hängt von der Leitungslänge und der Beschaltung am Leitungsende ab.

Prüfungsfrage

TH302  Eine Übertragungsleitung gilt als richtig angepasst, wenn der Widerstand, mit dem sie abgeschlossen ist,
	den Wert des Wellenwiderstandes aufweist.
	50 Ohm beträgt.
	reell ist.
	eine offene Leitung darstellt.

Der Wellenwiderstand ist der wichtigste Kennwert einer Hochfrequenzleitung. Sowohl die Antenne mit ihrem Fußpunktwiderstand wie auch der Sender mit seinem Ausgangswiderstand müssen mit dem dazwischen geschalteten Wellenwiderstand des Kabels übereinstimmen. Andernfalls gibt es Fehlanpassungen, die sich durch so genannte stehende Wellen äußern und zu Fehlverhalten führen.

Anders ausgedrückt: Schließt man an das Ende einer Hochfrequenzleitung einen Widerstand an, der genau dem Wert des Wellenwiderstandes entspricht, wird alle Leistung an diesen Widerstand abgegeben. Es treten keine Reflexionen und damit keine stehende Wellen auf. Deshalb definiert man:

Der Wellenwiderstand entspricht dem Abschlusswiderstand einer Leitung, bei dem keine stehenden Wellen auftreten.

Umgekehrt gilt: Treten stehende Wellen auf, ist der am Kabelanfang zu messende Widerstand nicht gleich dem Wellenwiderstand.

Bild 10-2: a) offene Paralleldrahtleitung, b) Flachbandleitung, c) Koaxialkabel

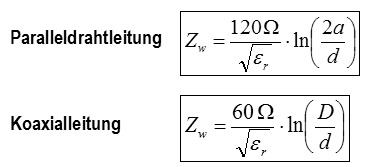
Der Wellenwiderstand der Leitung kann auch aus den geometrischen Abmessungen berechnet werden, also aus Durchmesser und Abstand der Leiter sowie dem Isolierstoff. Die Formeln zur überschlägigen Berechnung der Wellenwiderstände aus den mechanischen Abmessungen und dem Isolierstoff lauten:

a ist der Mittenabstand der Leiter, d ist der Durchmesser der Leiter bzw. Innenleiter, D ist der Innendurchmesser der Außenleiter, ε_r ist die relative Dielektrizitätszahl. Für Luft zwischen den Leitern ist ε_r = 1. Wenn Wasser in das Kabel eindringt, verändert sich der Wellenwiderstand, denn Wasser hat ein ε_r von 60 bis 80.

Prüfungsfrage

TH315  Ein Koaxialkabel hat einen Innendurchmesser von 0,7 mm. Die Isolierung zwischen Innenleiter und Abschirmgeflecht besteht aus Polyethylen (PE) und sie hat einen Durchmesser von 4,4 mm. Der Außendurchmesser des Kabels ist 7,7 mm. Wie hoch ist der (ungefähre) Wellenwiderstand des Kabels?
	ca. 20 Ω
	ca. 50 Ω
	ca. 75 Ω
	ca. 95 Ω

Lösung: In der Formelsammlung der BNetzA findet man für Polyethylen (PE) ε_r = 2,29. Der Innendurchmesser des Koaxkabels ist gleich dem Durchmesser der Isolierung. Die 7,7 mm Außendurchmesser braucht man für die Berechnung nicht.

Prüfungsfrage

TH316  Eine offene Paralleldrahtleitung ist aus Draht mit einem Durchmesser von 2 mm gefertigt. Der Abstand der Leiter beträgt 20 cm. Wie hoch ist der Wellenwiderstand der Leitung?
	ca. 276 Ω
	ca. 635 Ω
	ca. 820 Ω
	ca. 2,8 kΩ

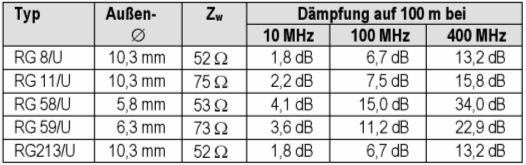
Lösung: Für Luft ist e_r = 1.

Die Wellenwiderstände Z_w der Hochfrequenzleitungen sind also vom Aufbau und vom Material abhängig. In der Praxis findet man folgende Werte.

Paralleldrahtleitungen         Z_w = 150 Ω bis 600 W

Koaxialleitungen                 Z_w =  50 Ω bis 125 Ω

Prüfungsfrage

TH303  Im Amateurfunk übliche Koaxialkabel weisen typischerweise Wellenwiderstände von
	50, 60 und 75 Ω auf.
	50, 300 und 600 Ω auf.
	60, 120 und 240 Ω auf.
	50, 75 und 240 Ω auf.

Prüfungsfrage

TH317  Ein Koaxialkabel (luftisoliert) hat einen Innendurchmesser der Abschirmung von 5 mm. Der Außendurchmesser des inneren Leiters beträgt 1 mm. Wie groß ist der Wellen­widerstand Z0 des Kabels?
	ca. 50 Ω
	ca. 60 Ω
	ca. 97 Ω
	ca. 120 Ω

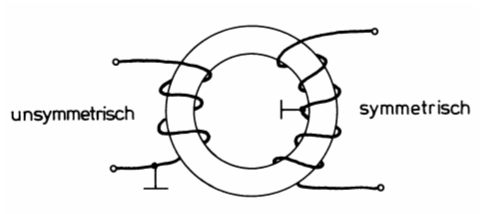
Paralleldrahtleitungen nennt man auch symmetrische Leitungen, weil Hinleiter und Rückleiter gleich geformt sind. Dadurch sind auch die Kapazitäten gegen Erde genau gleich. Koaxialleitungen sind unsymmetrisch, denn der Außenleiter ist anders geformt als der Innenleiter. Außerdem liegt der Außenleiter auf Erdpotential und der Innenleiter führt Hochfrequenz. Das Koaxkabel hat den Vorteil, dass wegen der Abschirmung unerwünschte Ausstrahlungen vermieden werden.

Prüfungsfrage

TH313  Wann ist eine Speiseleitung asymmetrisch?
	Wenn die beiden Leiter unterschiedlich geformt sind, z.B. Koaxialkabel.
	Wenn die hin- und zurücklaufende Leistung verschieden sind.
	Wenn sie außerhalb ihrer Resonanzfrequenz betrieben wird.
	Wenn die Koaxial-Leitung Spannung gegen Erde führt.

Prüfungsfrage

TH314  Bei einer Leitung mit symmetrischer Übertragung
	sind die Impedanzen bei beiden Leitern gegen Erde unendlich hoch.
	liegt einer der beiden Leiter auf Erdpotential.
	ist Strom und Spannung in den beiden Leitern gegenüber Erde gleich groß und gegenphasig.
	ist Strom und Spannung in den beiden Leitern gegenüber Erde gleich groß und gleichphasig.

Prüfungsfrage

TH324  Welche Leitungen sollten für die HF-Verbindungen zwischen Einrichtungen in der Amateurfunkstelle verwendet werden, um unerwünschte Abstrahlungen zu vermeiden?
	Unabgestimmte Speiseleitungen
	Symmetrische Feederleitungen
	Hochwertige asymmetrische Koaxialkabel
	Hochwertige abgeschirmte Netzanschlusskabel

Prüfungsfrage

TH323  Wie verhält sich das Stehwellenverhältnis, wenn Wasser in eine genau angepasste Antennenspeiseleitung eindringt?
	Es nimmt ab.
	Es erhöht sich.
	Es fällt auf 1:1 ab.
	Es bleibt konstant.

Der Verkürzungsfaktor

Die durch das Dielektrikum des Isolierstoffes vergrößerte Leitungskapazität bewirkt eine gegenüber der Lichtgeschwindigkeit etwa 10 bis 40 % geringere Ausbreitungsgeschwindigkeit von Strom- und Spannungsänderungen auf einer Leitung. Die Ausbreitungsgeschwindigkeit kann ebenfalls mit Hilfe von L und C der Leitung berechnet werden.

L’ und C’ bedeutet Induktivitätsbelag bzw. Kapazitätsbelag, also die Größen pro Meter Länge.

Beispiel
Von einer 1 m langen Leitung wird eine Induktivität von 1,5 µH und eine Kapazität von 20 pF gemessen. Wie groß ist die Ausbreitungsgeschwindigkeit auf dieser Leitung?

Lösung:

Durch diese geringere Ausbreitungsgeschwindigkeit ist auch die Wellenlänge auf Leitungen entsprechend kürzer. Das Verhältnis von Ausbreitungsgeschwindigkeit v einer Leitung zur Lichtgeschwindigkeit c bezeichnet man als Verkürzungsfaktor k.

Da sich die Ausbreitungsgeschwindigkeit auf der Leitung und die Lichtgeschwindigkeit nur durch die Dielektrizitätszahl der Leitungsisolation unterscheiden, kann man daraus direkt den Verkürzungsfaktor berechnen.

Prüfungsfrage

TH320  Der Verkürzungsfaktor eines Koaxialkabels mit einem Dielektrikum aus massivem Polyäthylen beträgt ungefähr
	0,66.
	0,1
	0,8
	1,0

Lösung: Aus der Formelsammlung entnehmen wir e_r = 2,29.

Diesen Verkürzungsfaktor von normalem Koaxkabel sollten Sie sich (nicht nur für die Prüfung) merken. Typische Verkürzungsfaktoren gebräuchlicher Antennenkabel sind in folgender Tabelle dargestellt.

Prüfungsfrage

TH322  Welche mechanische Länge hat ein λ/4 langes Koaxkabel mit Vollpolyethylenisolierung bei 145 MHz?
	17 cm
	34,2 cm
	51,7 cm
	1,03 m

Lösungsweg: Wir berechnen die Wellenlänge in Luft, nehmen davon ein Viertel und multi­plizieren mit dem Verkürzungsfaktor 0,66. Den Verkürzungsfaktor für PE mit 0,66 haben Sie sich ja gemerkt!

Prüfungsfrage

TA125  Der Verkürzungsfaktor ist
	das Verhältnis der Ausbreitungsgeschwindigkeit entlang eines Leiters zur Ausbreitungsgeschwindigkeit im Vakuum.
	das Verhältnis von Durchmesser zur Länge eines Leiters.
	das Verhältnis des Wellen- bzw. des Strahlungswiderstandes zum Feldwellenwiderstand des freien Raumes.
	die Wurzel aus dem Verhältnis von Induktivität zur Kapazität eines Leiters.

Prüfungsfrage

TH318  Die Ausbreitungsgeschwindigkeit in einem Koaxialkabel
	ist geringer als im Freiraum
	ist höher als im Freiraum.
	entspricht der Geschwindigkeit im Freiraum.
	ist fast unbegrenzt.

Prüfungsfrage

TH319  Der Verkürzungsfaktor einer luftisolierten Paralleldrahtleitung ist
	0,1.
	ungefähr 1.
	0,66.
	unbestimmt.

Prüfungsfrage

TH321  Wie lang ist ein Koaxialkabel, das für eine ganze Wellenlänge bei 100 MHz zugeschnitten wurde, wenn der Verkürzungsfaktor 0,6 beträgt?
	0,18 m
	1,8 m
	3 m
	6 m

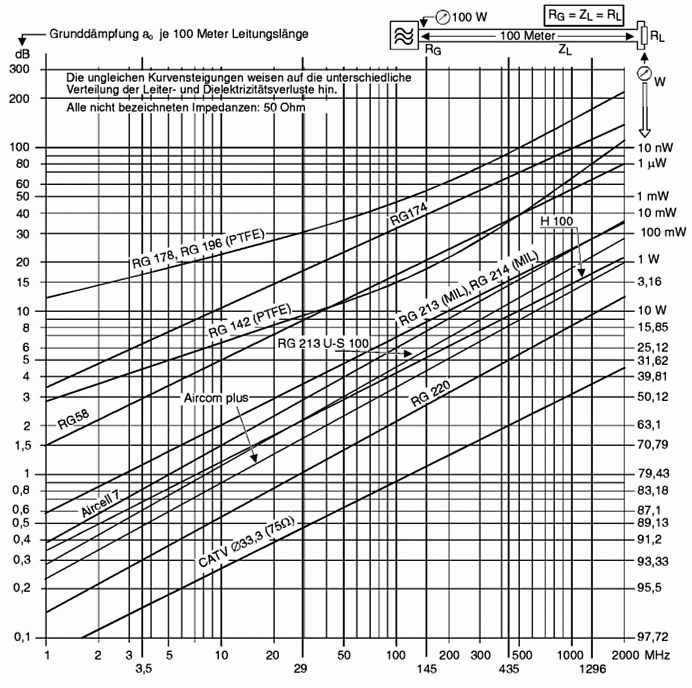
Die Dämpfung

Ein weiterer wichtiger Kennwert einer Hochfrequenzleitung ist die Dämpfung. Dämpfung bedeutet, dass nur noch ein Teil der Eingangshochfrequenzleistung am Ende der Leitung ankommt. Natürlich will man die Dämpfung in der Übertragungstechnik gering halten.

Die Dämpfung hängt vom Verlustwiderstand der Leitung ab. Das ist primär der Leitungswiderstand der inneren Kupferleitung und des Geflechtes bei Koaxkabeln. Je dicker der Innenleiter ist, desto geringer sind die Verluste. Desto dicker muss aber auch der Außenleiter sein. Diese Kabel sind teurer als dünne Leitungen.

Ferner hängen die Verluste vom Isolierstoff (Dielektrikum) ab. Am wenigsten Verluste haben Leitungen ohne Kunststofffüllung, also Luft als Dielektrikum. Diese Leitungen sind bei gleichem Innenleiter viel dicker. Sie sind aufwendiger in der Herstellung und dadurch teurer.

Die Dämpfung wird meist in dB pro 100 m Länge bei einer bestimmten Frequenz angegeben.  Verwendet man  ein  Kabel  mit halber Länge, hat man auch nur die Hälfte der Dämpfung. Beim Aufbau der Antenne sollte man also darauf achten, dass der Weg vom Sender bis zur Antenne möglichst kurz wird.

Die Dämpfung in dB verändert sich ungefähr mit der Wurzel der Frequenzverhältnisse.

Beispiel
Für ein Koaxkabel RG 213/U wird gemäß folgender Tabelle bei 100 MHz eine Dämpfung von 6,7 dB angegeben. Wie groß ist die Dämpfung bei 145 MHz?

Lösung:

Bei 145 MHz ist die Dämpfung also

1,2 ^. 6,7 dB = 8 dB

Manchmal montiert man deshalb bei sehr hohen Frequenzen die Senderendstufe direkt oben an der Antenne und führt die Stromversorgung über eine Außenleitung zu.

In der Formelsammlung der BNetzA finden Sie ein Diagramm mit der Grunddämpfung gebräuchlicher Koaxleitungen in Abhängigkeit der Betriebsfrequenz. Dieses Diagramm

Tabelle 10-1: Wellenwiderstand und Dämpfung gebräuchlicher Standard-Koaxkabel

haben Sie bereits im Lehrgang zur Klasse E kennen gelernt. Es soll noch einmal damit etwas geübt werden, weil es viele Prüfungsfragen dazu gibt.

Prüfungsfrage

TH304  Welche Dämpfung hat ein 15 m langes Koaxialkabel vom Typ RG58 bei 145 MHz?
	3 dB
	1,3 dB
	0,8 dB
	4,5 dB

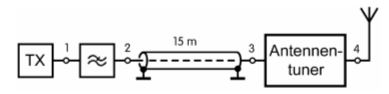
Lösung: Diagramm Kabeldämpfung. Bei 145 MHz ist bereits eine Linie eingetragen. Gehen Sie diese Linie hoch bis Sie die schräg verlaufende Linie RG58 treffen. Von diesem Schnittpunkt gehen Sie nach links und lesen den Wert für 100 m ab: 20 dB. Da es nur 15 m sind, müssen Sie diesen Wert mit 15/100 ins Verhältnis setzen.

Prüfungsfrage

TH305  Welche Dämpfung ergibt sich auf der Grundlage des Kabeldämpfungsdiagramms für ein 15-m-langes Koaxialkabel vom Typ RG58 bei 435 MHz?
	1,4 dB
	8,1 dB
	2,3 dB
	5,4 dB

Hinweis: Lösungsweg siehe vorige Aufgabe!

Prüfungsfrage

TH306  Welche Dämpfung ergibt sich auf der Grundlage des Kabeldämpfungsdiagramms für ein 25-m-langes Koaxialkabel vom Typ RG213 (MIL) bei 3,5 MHz?
	0,1 dB
	1,2 dB
	0,6 dB
	0,3 dB

Prüfungsfrage

TH307  Welche Dämpfung ergibt sich auf der Grundlage des Kabeldämpfungsdiagramms für ein 25-m-langes Koaxialkabel vom Typ RG213U-S100 bei 29 MHz?
	0,5 dB
	2,1 dB
	1,1 dB
	0,2 dB

Prüfungsfrage

TH308  Welche Dämpfung ergibt sich auf der Grundlage des Kabeldämpfungsdiagramms für ein 25-m-langes Koaxialkabel vom Typ RG213 (MIL) bei 145 MHz?
	2,2 dB
	8,7 dB
	4,4 dB
	0,9 dB

Prüfungsfrage

TH309  Welche Dämpfung ergibt sich auf der Grundlage des Kabeldämpfungsdiagramms für ein 25-m-langes Koaxialkabel vom Typ RG213U-S100 bei 435 MHz?
	1,1 dB
	11,0 dB
	5,5 dB
	2,8 dB

Prüfungsfrage

TH310  Welche Dämpfung ergibt sich auf der Grundlage des Kabeldämpfungsdiagramms für ein 25-m-langes Koaxialkabel vom Typ RG213U-S100 bei 1296 MHz?
	5,3 dB
	21,0 dB
	10,5 dB
	2,1 dB

Prüfungsfrage

TH311  Welches der folgenden Kabel weist im Kurzwellenbereich den geringsten Verlust auf?
	Kunststoffisolierte Zweidrahtleitung
	Koaxialkabel mit Vollisolation
	UKW-Bandleitung
	Offene Zweidrahtleitung

Prüfungsfrage

TH312  Welche Vorteile hat eine Paralleldraht-Speiseleitung?
	Sie hat geringere Dämpfung als andere Speiseleitungen und hohe Spannungsfestigkeit.
	Sie vermeidet Mantelwellen durch Wegfall der Abschirmung.
	Sie erlaubt leichtere Kontrolle des Wellenwiderstandes durch Verschieben der Spreizer.
	Sie bietet guten Blitzschutz durch niederohmige Drähte.

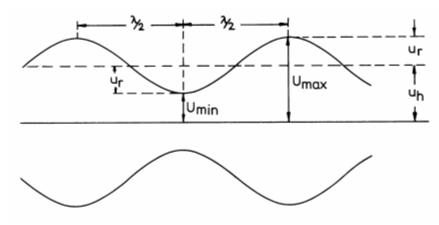
Das Stehwellenverhältnis SWR

Wie gut eine Antenne an die Zuleitung oder die Zuleitung an den Senderausgang angepasst ist, kann man mit dem Stehwellenverhältnis (SWR) beschreiben. Schickt man hochfrequente Leistung auf ein Kabel und wird wegen einer Fehlanpassung der Antenne an das Kabel nicht alle Energie abgenommen, wird dieser Teil reflektiert und wandert wieder zurück in Richtung Sender. Dabei überlagert sich diese rücklaufende Welle mit der hinlaufenden Welle. Dadurch entstehen in regelmäßigen Abständen von λ/2 vom Leitungsende aus gerechnet Wellenberge (u_h+u_r) und Wellentäler (u_h - u_r).

Bild 10-3: Maxima und Minima durch stehende Wellen

Das Verhältnis von maximaler Spannung (U_max) zu minimaler Spannung (U_min) nennt man Welligkeit s oder Stehwellenverhältnis SWR oder auch VSWR (voltage standing wave ratio).

Die Höhe der reflektierten Spannung u_r und damit U_max und U_min hängt direkt vom Grad der Fehlanpassung, also vom Verhältnis Abschlusswiderstand R_a (Antennenwiderstand) zum Wellenwiderstand Z_w der Zuleitung ab. Ist der Eingangswiderstand der Antenne größer als der Wellenwiderstand des Kabels, gilt folgende Formel

ansonsten gilt

Beispiel
Wie groß ist das Stehwellenverhältnis, wenn ein 50-Ω-Kabel mit einem Widerstand von  a) 100 Ω,  b) 10 Ω abgeschlossen wird?

Lösungen:

Prüfungsfrage

TH221  Ein Kabel mit einem Wellenwiderstand von 75 Ohm wird zur Speisung eines Faltdipols verwendet. Welche Welligkeit s kann man auf der Leitung erwarten?
	0,3
	ca. 1,5 bis 2
	ca. 3,2 bis 4
	5,7

Lösung: Ein Faltdipol hat eine Impedanz zwischen 240 und 300 Ohm.

Prüfungsfrage

TJ824  Zur Überprüfung eines Stehwellenmessgerätes wird dessen Ausgang mit einem 150-Ω-Widerstand abgeschlossen. Welches Stehwellenverhältnis muss das Messgerät anzeigen, wenn die Impedanz von Messgerät und Sender 50 Ω beträgt?
	2
	2,5
	3
	3,33

Das Stehwellenverhältnis lässt sich mit so genannten Richtkopplern oder SWR-Brücken messen (Mehr dazu in der Lektion 16: Messtechnik). Solch ein Stehwellenmessgerät misst die Spannung der Summe im Verhältnis zur Differenz der gemessenen Werte. Allerdings wird nicht die wirkliche Spannung gemessen, sondern nur ein Teil davon. Es soll nun eine Formel abgeleitet werden, mit der man das Stehwellenverhältnis aus dieser Spannungsmessung berechnen kann.

Mit einem Richtkoppler misst man die hinlaufende und die rücklaufende Spannung. Aus dem Verhältnis von Summe und Differenz berechnet man das SWR.

Beispiel
Mit einem Richtkoppler wurde die hinlaufende Spannung mit 1 V gemessen und die rücklaufende mit 0,5 V. Wie groß ist das Stehwellenverhältnis?

Lösung:

Wenn die Hälfte der Spannung reflektiert wird, ergibt sich ein Stehwellenverhältnis von 3. Für den Sonderfall, dass keine Hochfrequenz reflektiert wird, ergibt sich folgendes Verhältnis.

Merken Sie sich: Bei einem Stehwellenverhältnis von 1 (bzw. 1:1) liegt optimale Anpassung vor.

Prüfungsfrage

TJ404  Ein Stehwellenmessgerät wird in ein ideal angepasstes Sender-/Antennensystem eingeschleift. Das Messgerät sollte
	ein Stehwellenverhältnis von 1:1 anzeigen.
	einen Rücklauf von 100% anzeigen.
	ein Stehwellenverhältnis von 1:0 anzeigen.
	ein Stehwellenverhältnis von 0:1 anzeigen.

Aufgabe
Mit einem Vorwiderstand von 1 kΩ wurde ein Strommesser zu einem Spannungsmesser erweitert. Berechnen Sie das Stehwellenverhältnis, wenn für die Summenspannung ein Wert von 100 (µA) und für die Differenzspannung ein Wert von 33,3 (µA) gemessen wurde.

Bild 10-4: Skala eines Stehwellenmessgerätes

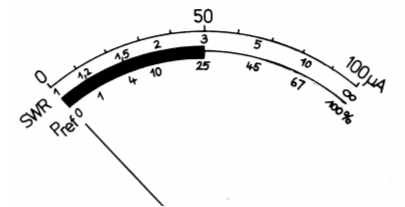
Ob Strom oder Spannung - die Berechnung bleibt gleich. Trägt man für alle möglichen Verhältnisse das SWR in eine Skala eines Messgerätes ein, kann man ohne weitere Rechnung das SWR direkt ablesen.

Ableseübung
Wie groß ist das SWR, wenn der Zeigerausschlag bei
a) 10,   b) 20,   c) 33,   d) 50   e) 66 (µA) steht?

Lösungen: a) 1,2  b) 1,4  c) 2  d) 3  e) 4,9

Prüfungsfrage

TH220  Eine VHF-Antenne hat ein Stehwellenverhältnis (VSWR) von 3. Wie viel Prozent der Sendeleistung wird von der Antenne abgestrahlt, wenn sonst keine weiteren Verluste auftreten und keine Anpassung erfolgt?
	25%
	29%
	50%
	75%

Lösung: Bei einem SWR von 3 wird genau die Hälfte der Spannung reflektiert. Die Hälfte der Spannung bedeutet wegen des quadratischen Zusammenhangs ein Viertel der Leistung. 75 % bleibt also für die Abstrahlung übrig. Sie sehen auf der Skala des gezeichneten SWR-Meters auch eine Skala für reflektierte Leistung.
Bei SWR=3 steht P_ref = 25 %.

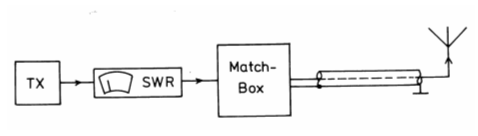
Das Stehwellenmessgerät wird an der Stelle einer Antennenanlage eingeschleift, wo das SWR bestimmt werden soll. Möchte man die Antenne selbst überprüfen, setzt man das SWR-Meter zwischen Antennenkabel und Antenneneingang. Möchte man mit einem Universalanpassgerät (Matchbox) eine Antennenanlage inklusive Kabel anpassen, sieht es folgendermaßen aus.

Bild 10-5: Einsatz des SWR-Meters bei Verwendung einer Matchbox

Prüfungsfrage

TJ822  Ein Stehwellenmessgerät wird bei Sendern zur Messung
	der Bandbreite eingesetzt.
	der Oberwellenausgangsleistung eingesetzt.
	der Antennenanpassung eingesetzt.
	des Wirkungsgrades eingesetzt.

Prüfungsfrage

TJ823  An welchem Punkt sollte das Steh­wellenmessgerät eingeschleift werden, um zu prüfen, ob der Sender gut an die Antennenanlage angepasst ist?
	Punkt 1
	Punkt 2
	Punkt 3
	Punkt 4

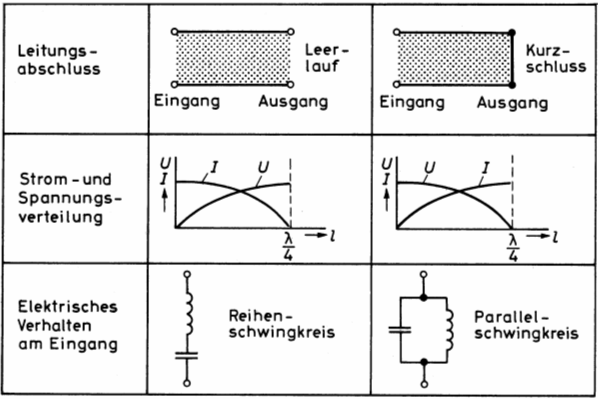
Die Lecherleitung

Ein Sonderfall einer Transformationsleitung ist der Abschluss einer Leitung mit dem Widerstandswert Null (Kurzschluss) oder dem Widerstandswert Unendlich (Leerlauf). Dies nennt man eine Lecherleitung. Eine Lecherleitung ist ein kurzes, verlustloses Leitungsstück, das entweder im Leerlauf oder im Kurzschluss betrieben wird.

Bild 10-6: Kurzgeschlossene Lecherleitung

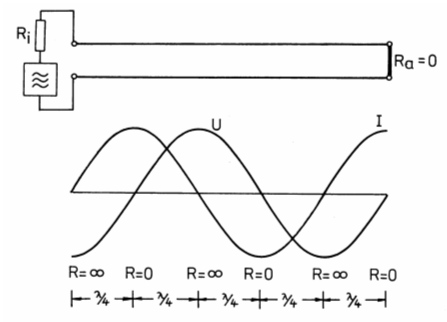
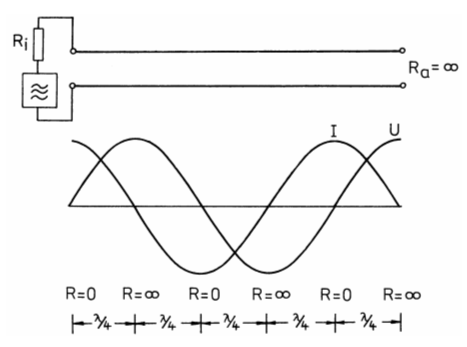
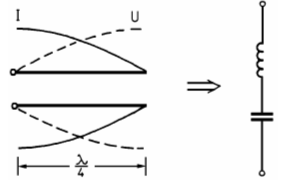
Gibt man eine hochfrequente Wechselspannung auf eine Doppelleitung, die am Ende kurzgeschlossen ist, wird sämtliche Energie wieder reflektiert (SWR unendlich) und es gibt Auslöschungen und Anhebungen wie im Bild 10-6 zu sehen ist. Am Ende ist wegen des Kurzschlusses die Spannung Null, der Strom hat jedoch sein Maximum. Nach jeweils λ/4 vom Leitungsende kehren sich die Verhältnisse um. Dies entspricht der Strom- und Spannungsverteilung auf Antennen, wie dies in Lektion 14 bereits gezeigt wurde.

Betrachtet man das Verhältnis U/I entlang dieser Leitung, erkennt man, dass dieser Widerstand nicht an allen Stellen gleich ist, wie dies bei einer angepassten Leitung der Fall wäre. Am Ende hat die Leitung den Widerstand R = 0. Bei λ/4 und wieder bei ¾-λ dagegen ist der Widerstand unendlich hoch. Dazwischen ergibt sich wechselweise kapazitives oder induktives Verhalten.

Lässt man die Leitung am Ende offen, ergeben sich die umgekehrten Verhältnisse. Am Ende dieser Leitung ist der Strom Null, während die Spannung ihren Höchstwert hat.

Bild 10-7: Offene Lecherleitung

Bild 10-8: λ/4-Leitung als Schwingkreis

Ergibt sich bei einer Frequenz ein sehr großer Widerstand, entspricht dies dem Verhalten eines Parallelschwingkreises. Wird der Widerstand sehr klein, liegt das Verhalten eines Serienschwingkreises vor. Bei hohen Frequenzen kann man also Lecherleitungen als Schwingkreise verwenden.

Bei kurzgeschlossenem Ende ist der Eingangswiderstand einer λ/4-Leitung sehr groß. Verändert man die Frequenz der anliegenden HF-Spannung, nimmt der Widerstand ab. Dieses elektrische Verhalten entspricht einem Parallelschwingkreis. Bei offenem Ende (Leerlauf) sind die Verhältnisse umgekehrt. Der Eingangswiderstand wird niederohmig. Dies entspricht dem Verhalten eines Serienschwing­kreises (Reihenschwingkreis).

Prüfungsfrage

TH325  Eine Lecherleitung besteht aus zwei parallelen Leitern. Wovon ist ihre Resonanzfrequenz wesentlich abhängig?  Sie ist abhängig
	vom Wellenwiderstand der beiden parallelen Leiter.
	vom verwendeten Abschlusswiderstand.
	vom Leerlauf-Kurzschlussverhalten.
	von der Leitungslänge

Prüfungsfrage

TH326  Was zeigt diese Darstellung?
	Sie zeigt die Strom- und Spannungsverteilung an einer offenen λ/4-Lecherleitung. Sie wirkt als Reihenschwingkreis.
	Sie zeigt die Strom- und Spannungsverteilung an einer Antennenspeiseleitung. Die Antenne arbeitet als Serienresonanzkreis.
	Sie zeigt die Strom- und Spannungsverteilung an einer Antenne. Die Antenne arbeitet als Groundplane mit Verkürzungskondensator.
	Sie zeigt die Strom- und Spannungsverteilung an den Radialen einer Groundplane. Die Antenne arbeitet mit Verlängerungsspule zur Resonanzanpassung.

Anstelle von Lambdaviertel-Leitungen kann man auch Leitungen mit der Länge λ/2 als Schwingkreise betreiben. Die Verhältnisse kehren sich dabei um. Eine am Ende kurzgeschlossene Lambdahalbeleitung hat das gleiche elektrische Verhalten wie eine am Ende offene λ/4-Leitung. Einfacher ausgedrückt: Eine λ/2-Leitung hat am Eingang das elektrische Verhalten des Endes, also Kurzschluss am Ende, ergibt Kurzschluss am Eingang und umgekehrt.

Bei Frequenzen oberhalb 500 MHz, also beispielsweise im 23-cm-Band, werden Schwingkreise ausschließlich in dieser Leitungstechnik ausgeführt. In realen Spulen und Kondensatoren wären die Verluste viel höher.

Zusammenfassung

Eine Lambdaviertelleitung kehrt die Impedanzverhältnisse um
(niederohmig - hochohmig). Sie wirkt wie ein Schwingkreis.

Eine Lambdahalbeleitung transformiert 1 : 1, wirkt auch wie ein Schwingkreis.

Prüfungsfrage

TH403  Einem Ganzwellendipol wird die Sendeleistung über eine abgestimmte λ/4-Speiseleitung zugeführt. Wie groß ist die Impedanz Z1 am Einspeisepunkt des Dipols? Und wie groß ist die Impedanz Z2 am Anfang der Speiseleitung?
	Z1 und Z2 sind hochohmig.
	Z1 ist hochohmig und Z2 niederohmig.
	Z1 und Z2 sind niederohmig.
	Z1 ist niederohmig und Z2 hochohmig.

Prüfungsfrage

TH404  Einem Ganzwellendipol wird die Sendeleistung über eine abgestimmte  l/2-Speiseleitung zugeführt. Wie groß ist die Impedanz Z1 am Einspeisepunkt des Dipols? Und wie groß ist die Impedanz Z2 am Anfang der Speiseleitung?
	Z1 und Z2 sind niederohmig.
	Z1 ist niederohmig und Z2 hochohmig.
	Z1 und Z2 sind hochohmig.
	Z1 ist hochohmig und Z2 niederohmig.

Prüfungsfrage

TH405  Einem Halbwellendipol wird die Sendeleistung über eine abgestimmte  λ/2-Speiseleitung zugeführt. Wie groß ist die Impedanz Z1 am Einspeisepunkt des Dipols? Und wie groß ist die Impedanz Z2 am Anfang der Speiseleitung?
	Z1 und Z2 sind niederohmig.
	Z1 und Z2 sind hochohmig.
	Z1 ist niederohmig und Z2 hochohmig.
	Z1 ist hochohmig und Z2 niederohmig.

Prüfungsfrage

TH408  Wie groß ist die Impedanz am Punkt X, wenn die elektrische Länge der abgebildeten Leitung λ/4 beträgt?
	Annähernd 0 Ohm
	Sehr hochohmig
	50 Ohm
	Ungefähr 100 Ohm

Tipp: Aus Kurzschluss wird nach Lambda-Viertel Leerlauf.

Prüfungsfrage

TH409  Wie groß ist die Impedanz am Punkt X, wenn die elektrische Länge der abgebildeten Leitung λ/4 beträgt?
	Sehr hochohmig
	Annähernd 0 Ohm
	50 Ohm
	Ungefähr  100 Ohm

Tipp: Aus Leerlauf wird nach Lambda-Viertel Kurzschluss.

Prüfungsfrage

TH410  Eine Viertelwellen-Übertragungsleitung ist an einem Ende offen. Die Impedanz am anderen Ende
	ist nahezu unendlich hoch.
	ist gleich dem Wellenwiderstand.
	beträgt das Dreifache des Wellenwiderstandes.
	beträgt nahezu Null.

Prüfungsfrage

TH413  Eine Halbwellen-Übertragungsleitung ist an einem Ende mit 50 Ohm abgeschlossen. Wie groß ist die Eingangsimpedanz am anderen Ende dieser Leitung?
	25 Ω
	50 Ω
	100 Ω
	200 Ω

Prüfungsfrage

TH414  Ein Halbwellendipol hat an seinem Einspeisepunkt eine Impedanz von 70 Ω. Er wird über ein λ/2-langes 300-Ω-Flachbandkabel gespeist. Wie groß ist die Impedanz am Eingang der Speiseleitung?
	70 Ω
	185 Ω
	300 Ω
	370 Ω

Eine Lambdaviertelleitung kann auch sehr gut als Phasenschieber verwendet werden. In einer Viertelwelle haben wir genau eine Phasenverschiebung von 90 Grad (von Maximum bis Minimum oder umgekehrt). Für eine Erregung von zwei Antennen in zirkularer Polarisation wird eine Phasenverschiebung von 90 Grad gebraucht. Dafür lässt sich also solch eine Lambdaviertelleitung verwenden.

Prüfungsfrage

TH411  Welche Phasenverschiebung erhält ein HF-Signal von A nach B, wenn die elektrische Länge der abgebildeten Leitung λ/4 beträgt?
	Null
	180°
	π/4
	90°

Prüfungsfrage

TH412 Welche Phasenverschiebung erhält ein HF-Signal von A nach B, wenn die elektrische Länge der abgebildeten Leitung gleich der Wellenlänge ist?
	π/4
	180°
	2 π
	90°

Tipp zu TH412: 360 Grad entsprechen 2 π.

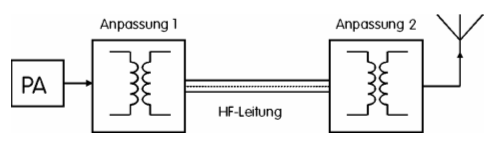
Transformationsleitungen

Transformationsleitungen dienen der Anpassung. Anpassung in der Hochfrequenztechnik bedeutet, dass man einerseits den Arbeits- oder Außenwiderstand des Senders an die angeschlossene HF-Leitung und andererseits die Antennenimpedanz an das Antennenkabel anpassen muss.

Bild 10-9: Anpassung Sender - Kabel - Antenne

Die Transistoren oder Röhren einer Senderendstufe (PA, power amplifier) müssen bei eingangsseitig voller Aussteuerung und gegebener Betriebsspannung einen bestimmten Lastwiderstand R_L vorfinden, wenn sie die maximal mögliche Ausgangsleistung abgeben sollen. Die Größenordnung des optimalen R_L liegt bei Transistoren bei wenigen Ohm und bei Röhren bis zu einigen Kiloohm.

Mittels Anpassglieder wird der jeweilige Lastwiderstand R_L in den heute üblichen Senderausgangswiderstand von 50 Ohm transformiert. Wird nun an den 50-Ω-Ausgang ein Koaxialkabel mit einem Wellenwiderstand von 50 W angeschlossen, das seinerseits mit einer Antenne verbunden ist, deren Eingangswiderstand in der Nähe von 50 Ω liegt, gibt der Sender die maximal mögliche Leistung ab.

Weicht jedoch der Strahlungswiderstand der Antenne wesentlich von 50 Ω ab, etwa wegen zu geringer Aufbauhöhe oder weil man sich mit der Senderfrequenz wesentlich von der Resonanzfrequenz entfernt hat, findet die PA eine abweichende Impedanz vor und die Leistungsabgabe sinkt. Außerdem haben nicht resonante Antennen neben dem Wirkwiderstand noch einen Blindwiderstand, der kompensiert werden muss.

Im Bild 10-6 wurde gezeigt, dass bei einer am Ende offenen λ/4-Lecherleitung im Idealfall der Ausgangswiderstand unendlich und der Eingangswiderstand Null betragen. Die λ/4-Leitung hat also die Eigenschaft, einen hohen Widerstandswert auf einen niedrigen zu transformieren.

Schließt man eine λ/4-Leitung an einen beliebigen Widerstand an, der nicht dem Wellenwiderstand entspricht, entstehen stehende Wellen auf der Leitung und es ändert sich das Spannungs-Strom-Verhältnis im Verlauf einer Viertelwellenlänge.

Bild 10-10: Prinzip der Transformationsleitung

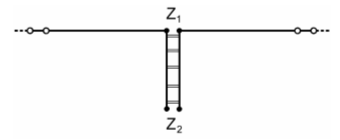
Die λ/4-Leitung kann also Widerstände transformieren, allerdings nur innerhalb einer begrenzten Bandbreite. Die Leitung wirkt als Transformator. Eine solche Leitung bestimmter Länge wird auch als abgestimmte Speiseleitung bezeichnet im Gegensatz zur unabgestimmten Speiseleitung, bei welcher die Leitung mit ihrem Wellenwiderstand abgeschlossen wird und keine Stehwellen entstehen.

Sollen zwei verschiedene Wellenwiderstände Z₁ und Z₂ aneinander angepasst werden, schaltet man eine λ/4-Leitung dazwischen, welche auch als Q-Match bezeichnet wird. Diese Transformationsleitung darf auch ein ungeradzahliges Vielfaches von λ/4 haben. Sie muss folgende Werte haben.

 

Wellenwiderstand    

Länge                 

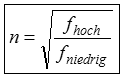
n ist eine ganze Zahl. Dieser Faktor (2n-1) bedeutet, dass nur ungeradzahlige Vielfache genommen werden können. Ist beispielsweise n=2, ergibt der Faktor 2 · 2 - 3 Normalerweise wird n=1 gewählt. Dann ist die Länge der Leitung genau

Länge                

k ist der Verkürzungsfaktor. Bei dem üblicherweise verwendeten Koaxkabel mit Vollisolation ist k = 0,66, wie Sie sich weiter oben gemerkt haben.

Beispiel
Welchen Wellenwiderstand und welche mechanische Länge muss eine λ/4-Transformationsleitung für eine Frequenz von 14,0 MHz haben, wenn eine Antennendrahtschleife (Loop) mit einer Impedanz von 100 Ω an ein Koaxkabel von 50 Ω angeschlossen werden soll?

Lösung

Prüfungsfrage

TH406  Ein Faltdipol mit einem Fußpunktwiderstand von 240 Ω soll mit einer Hühnerleiter gespeist werden, deren Wellenwiderstand 600 Ω beträgt. Zur Anpassung soll ein λ/4-langes Stück Hühnerleiter mit einem anderem Wellenwiderstand verwendet werden. Welchen Wellenwiderstand muss die Transformationsleitung haben?
	240 Ω
	420 Ω
	840 Ω
	380 Ω

Prüfungsfrage

TH407  Ein Dipol mit einem Fußpunktwiderstand von 60 Ω soll über eine λ/4-Transformationsleitung mit einem 240-Ω-Flachbandkabel gespeist werden. Welchen Wellenwiderstand muss die Transformationsleitung haben?
	120 Ω
	247 Ω
	232 Ω
	300 Ω

Lösung machen?

Bild 10-11: λ/4-Transformation zur Parallelschaltung von zwei Antennen

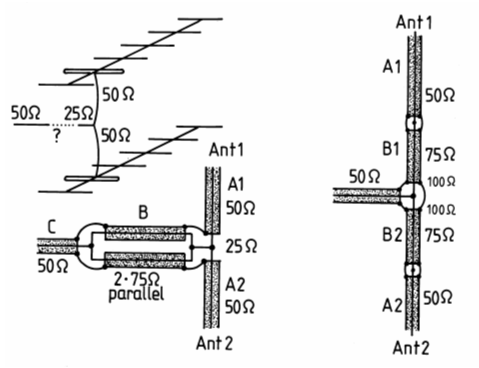
Ein anderes Beispiel für die Anwendung von λ/4-Transformationsleitungen ist in Bild 10-11 dargestellt. Zwei Antennen mit je 50 Ω Impedanz sollen gestockt werden. Die Antennenleitungen müssten zu diesem Zweck parallelgeschaltet werden. Bei der Parallelschaltung von zwei 50-Ω-Kabeln ergibt sich aber am Zusammenschaltpunkt die halbe Impedanz, also 25 Ω. Für die Lösung des Problems, diese Zusammenschaltung an ein gemeinsames Kabel anzupassen, gibt es mit Hilfe von λ/4-Transformationsleitungen zwei Lösungsmöglichkeiten.

Lösung A: Die gleich langen Ableitungsstücke A₁ und A₂ von der Antenne werden zunächst parallelgeschaltet. Um nun von 25 Ω auf 50 Ω zu kommen, muss eine λ/4-Transformationsleitung (B) mit einer Impedanz von

dazwischen geschaltet werden. Ein solches Kabel gibt es nicht. Man kann aber zwei Stücke von je 75 Ω parallel schalten und erhält dann 37,5 Ω, ungefähr der gewünschte Wert.

Lösung B: Die beiden 50-Ω-Antennenzu­leitungen werden je über eine λ/4-Trans­formationsleitung auf ca. 100 Ω transformiert und dann parallel geschaltet, um auf 50 Ω zu kommen. Es wird eine Impedanz benötigt von

Man kann dafür 75-Ω-Kabel verwenden.

Die Länge: In beiden Fällen benötigt man zwei Stücke Koaxkabel mit einer Länge von λ/4 mal Verkürzungsfaktor mit einem Wellenwiderstand von 75 Ω. Die Länge berechnet man mit den Formeln

Übungsaufgabe
ÜB10-1 Berechnen Sie die Länge einer λ/4-Transformationsleitung aus Koaxkabel mit Voll-PE-Isolation für die Frequenz f = 433 MHz.
A 11,4 cm              B 17,3 cm
C 45,7 cm              D 69,3 cm

Lösung:

Bild 10-12: Gruppe von 4 x 7 Element Yagis

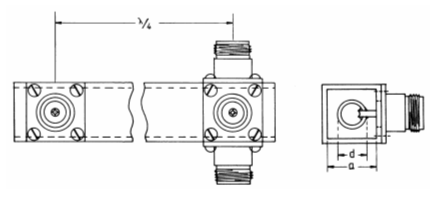
Viel einfacher können vier Antennen parallel geschaltet werden. Werden alle vier gleich langen Zuleitungsstücke parallel geschaltet, ergeben sich 50 : 4 = 12,5 Ohm. Die λ/4-Transformationsleitung von 12,5 auf 50 Ω benötigt eine Impedanz von

Man kann hierfür zwei Stücke mit je 50 Ω parallel schalten.

Eine Transformationsleitung mit einem beliebigen Wellenwiderstand lässt sich leicht selbst herstellen. Dafür werden einfach zwei Aluminium- oder Messingrohre ineinander gesteckt. Die Rohre müssen ein bestimmtes Durchmesserverhältnis zueinander haben. Als Berechnungsformel dient die Formel für den Wellenwiderstand einer Koaxialleitung.

Da Luft als Dielektrikum verwendet wird, fällt e_r weg. Stellt man die Formel nach D, dem Innendurchmesser des Außenrohres um, ergibt sich

Falls ein quadratisches Außenrohr verwendet wird, muss das Innenrohr 8 % dicker gemacht werden, wenn in obige Formel für den Durchmesser D das Innenmaß a des Rohres eingesetzt wird.

Bild 10-13: Anpasstopf mit quadratischem Rohr

Bild 10-14: Hühnerleiter (rechts im Bild)

 

Die Paralleldrahtleitung

Für die Einspeisung unabgestimmter symmetrischer Antennen eignet sich die Paralleldrahtleitung (im Amateurfunk „Hühnerleiter“ genannt) wegen ihrer geringen Verluste hervorragend als Speiseleitung. Man kann sie fertig im Amateurfunk-Zubehörhandel kaufen oder auch selbst anfertigen, indem man zwei Antennendrähte mit Isolierspreizern auf einen Abstand von zirka 10 cm bringt.

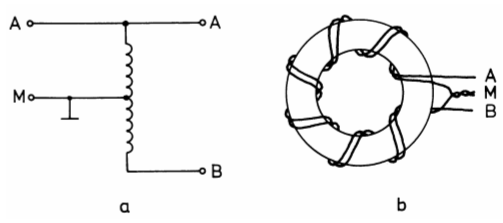
Die Symmetrierung

Außer der eigentlichen Widerstandsanpassung muss bei Speisung von symmetrischen Antennen mit unsymmetrischen Kabeln auch noch symmetriert werden. Symmetrische Antennen sind alle Arten von Dipolen, unsymmetrische Antennen sind solche, die gegen Erde erregt werden (λ/4-Verti­kalstrahler). Symmetrische Kabel sind Paralleldrahtleitungen, unsymmetrische Kabel sind Koaxialkabel.

Bild 10-15: Ringkern-Balun

Wird eine symmetrische Antenne direkt an ein Koaxkabel angeschlossen, so entstehen durch die Unsymmetrie Ausgleichsströme auf dem Mantel des Kabels, so genannte Mantelwellen. Damit strahlt ein solches  Kabel  HF-Energie ab,  was  bei benachbarten Zuleitungskabeln für Rundfunk- und Fernsehgeräte zu unerwünschten störenden Beeinflussungen führen kann. Zudem steigen die Verluste und das Strahlungsdiagramm der Antenne wird verzerrt.

Zur Symmetrierung wird ein Breitbandsymmetrierübertrager (Balun genannt) verwendet. Balun kommt aus dem Englischen von balanced (symmetrisch) - unbalanced (unsymmetrisch). Es gibt mehrere Möglichkeiten der Ausführung eines Baluns. Hier soll als Beispiel der Ringkern-Balun beschrieben werden.

Man benutzt einen Ringkern für eine gute Kopplung und baut damit einen HF-Transformator auf. Soll die Impedanz gleich bleiben, müssen Primär- und Sekundärwindungszahlen ebenfalls gleich sein. Erdet man die Mittelanzapfung auf der Sekundärseite, hat man bereits die Symmetrierung durchgeführt. Durch Verändern des Verhältnisses der Windungszahlen kann gleichzeitig auch noch eine Widerstandstransformation durchgeführt werden.

Bild 10-16: Ringkern-Balun-Transformator 1 : 4, a: Wickelschema, b: praktische Ausführung

Häufig wird hierbei das Prinzip des Spartransformators angewendet. Der Eingang ist an halber Windungszahl angeschlossen. Deshalb transformiert dieser Symmetrierübertrager im Verhältnis 1:2² = 1:4.

Praxis
Für eine gute Kopplung werden die Windungen ineinander gewickelt. Man fertigt hierfür eine zweiadrige (bifilare) Wicklung an und verbindet jeweils Anfang und Ende der beiden Drähte im Punkt M (Mitte, Masse), so dass eine Reihenschaltung von A nach B besteht.

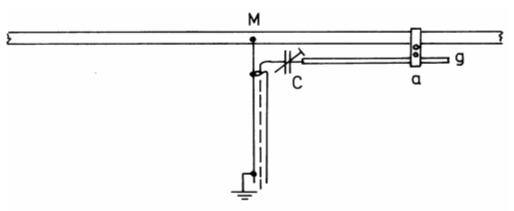
Im UKW-Bereich sind Ringkernübertrager wegen der erhöhten Verluste weniger geeignet. Hierfür gibt es eine Reihe anderer Anpassungsmöglichkeiten, von denen die Gammaanpassung beschrieben werden soll.

Bild 10-17: Gamma-Match

Die Gammaanpassung verwendet man, um einen symmetrischen Strahler (UKW-Yagi oder Kurzwellenbeam) unter Umgehung eines Baluns direkt mit dem Koaxkabel speisen zu können. Mit einer verschiebbaren Abgreif­schelle (a) wird ein im Vergleich zum Strahlerelement dünneres Gammarohr (g) gehalten. Die Seele des Kabels wird über einen Drehkondensator (C) an das Gammarohr und der Mantel des Kabels in Strahlermitte (M) angeschlossen. Man verschiebt zunächst die Abgreifschelle bei eingedrehtem Kondensator C, bis das beste SWR erreicht ist und kompensiert dann  mit

Bild 10-18: Lambdahalbe Umwegleitung

dem Drehkondensator die Blindkomponente bis wiederum das SWR den besten Wert erreicht. Für den VHF-UHF-Bereich kann man eine Lambdahalbe-Transformations­leitung auch zur Symmetrierung benutzen.

Das Prinzip ist folgendes. An der Einspeisestelle teilt sich der Strom je zur Hälfte auf. Eine Hälfte geht direkt zur Antenne die andere Hälfte in die Umwegleitung. Halber Strom bei gleicher Spannung ist doppelter Widerstand. Es ergeben sich also 100 Ohm, wenn man mit 50 Ohm einspeist. Die Lambdahalbe Umwegleitung stellt das Signal auf der anderen Seite noch einmal mit gleicher Impedanz von 100 Ohm zur Verfügung. Von jeder Seite bis zur Mitte 100 Ohm ergibt zusammen 200 Ohm.

Prüfungsfrage

TH401  Was zeigt diese Darstellung?
	Sie zeigt einen λ/2-Faltdipol mit λ/2-Umwegleitung. Durch die Anordnung wird der Fußpunktwiderstand der symmetrischen Antenne von 240 Ω an ein unsymmetrisches 60-Ω-Antennenkabel angepasst.
	Sie zeigt einen symmetrischen 60-Ω-Schleifendipol mit Koaxialkabel-Balun. Durch die Anordnung wird die symmetrische Antenne an ein unsymmetrisches 60-Ω-Antennenkabel angepasst.
	Sie zeigt einen λ/2-Dipol mit symmetrierender λ/2-Umwegleitung. Durch die Anordnung wird der Fußpunktwiderstand der symmetrischen Antenne von 120 Ω an ein unsymmetrisches 60-Ω-Antennenkabel angepasst.
	Sie zeigt einen symmetrischen 60-Ω-Schleifendipol mit einem koaxialen Leitungskreis, der als Sperrfilter zur Unterdrückung von unerwünschten Aussendungen eingesetzt ist.

Prüfungsfrage

TH402  Zur Anpassung von Antennen werden häufig Umwegleitungen verwendet. Wie arbeitet die folgende Schaltung?
	Der λ/2-Faltdipol hat an jedem seiner Anschlüsse eine Impedanz von 120 Ω gegen Erde. Durch die λ/2-Umwegleitung erfolgt eine 1:1 Widerstandstransformation mit Phasendrehung um 180°. An der Seite der Antennenleitung erfolgt eine phasenrichtige Parallelschaltung von 2 mal 120 Ω gegen Erde, womit eine Ausgangsimpedanz von 60 Ω erreicht wird.
	Der λ/2-Faltdipol hat eine Impedanz von 240 Ω. Durch die λ/2-Umwegleitung erfolgt eine 4:1 Widerstandstransformation mit Phasendrehung um 360°, womit an der Seite der Antennenleitung eine Ausgangsimpedanz von 60 Ω erreicht wird.
	Der λ/2-Dipol hat eine Impedanz von 60 Ω. Durch die λ/2-Umwegleitung erfolgt eine 1:2 Widerstandstransformation mit Phasendrehung um 180°. An der Seite der Antennenleitung erfolgt eine phasenrichtige Parallelschaltung von 2 mal 120 Ω gegen Erde. Womit eine Ausgangsimpedanz von 60 Ω erreicht wird.
	Der λ/2-Dipol hat eine Impedanz von 240 Ω. Durch die λ/2-Umwegleitung erfolgt eine 4:1 Widerstandstransformation mit Phasendrehung um 360°, womit an der Seite der Antennenleitung eine Ausgangsimpedanz von 60 Ω erreicht wird.

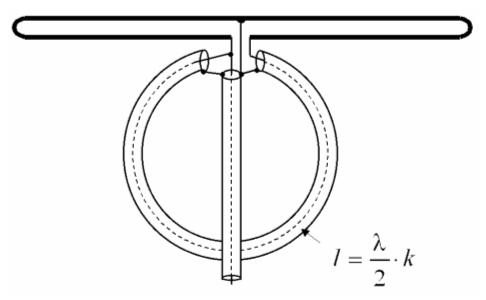
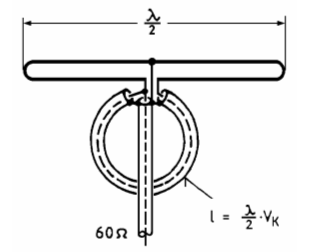
Wenn eine symmetrische Antenne (Dipol oder Beam) mit einem (unsymmetrischen) Koaxialkabel gespeist werden soll, muss man entweder ein Symmetrieglied verwenden oder man kann zur Vermeidung von dadurch auftretenden Mantelwellen (Ströme auf dem Außenmantel) eine so genannte Mantelwellendrossel einsetzen. Sie besteht aus einem Stück aufgewickeltem Koaxkabel gleicher Impedanz. Es wirkt wie ein Lambdahalbe-Transformator.

Aufgabe
Berechnen Sie die Länge einer Lambdahalbe-Transformationsleitung aus Koaxkabel mit Voll-PE-Isolation für einen Beam mit 14 MHz. Dieses Kabel soll anschließend aufgewickelt werden mit zirka 6 Windungen. Welchen Durchmesser müssen diese Windungen haben?

Lösung:

Bei 6 Windungen hat jede Windung 1,18 m Umfang. Den Umfang eines Kreises berechnet man mit l_umf = π·d, also ist

Wenn man die Wirkung verbessern möchte, kann man die Windungen des Kabels durch einen Ferrit-Ringkern ziehen.

Prüfungsfrage

TH415  Welche Auswirkungen hat es, wenn eine symmetrische Antenne (Dipol) mit einem Koaxkabel gleicher Impedanz gespeist wird?
	Die Richtcharakteristik der Antenne wird verformt und es können Mantelwellen auftreten.
	Es treten keine nennenswerten Auswirkungen auf, da die Antenne angepasst ist und die Speisung über ein Koaxkabel erfolgt, dessen Außenleiter Erdpotential hat.
	Am Speisepunkt der Antenne treten gegenphasige Spannungen und Ströme gleicher Größe auf, die eine Fehlanpassung hervorrufen.
	Es treten Polarisationsdrehungen auf, die von der Kabellänge abhängig sind.

Prüfungsfrage

TH416 Eine symmetrische Antenne (Dipol) soll mit einem unsymmetrischen Kabel (Koaxkabel) gleicher Impedanz gespeist werden. Dabei erreicht man einen Symmetriereffekt zum Beispiel
	durch Parallelschalten eines am freien Ende kurzgeschlossenen λ/2-langen Leitungsstücks (Stub) am Speisepunkt der Antenne.
	durch die Einfügung von Sperrkreisen (Traps) in den Dipol.
	durch Parallelschalten eines am freien Ende offenen λ/4-langen Leitungsstücks (Stub) am Speisepunkt der Antenne.
	durch Symmetrierglieder wie Umwegleitung oder Balun.

Prüfungsfrage

TH417 Auf einem Ferritkern sind etliche Windungen Koaxialkabel aufgewickelt. Diese Anordnung kann dazu dienen
	statische Aufladungen zu verhindern.
	eine Antennenleitung abzustimmen.
	Mantelwellen zu dämpfen.
	Oberwellen zu unterdrücken.

Prüfungsfrage

TH418 Ein symmetrischer Halbwellendipol wird direkt über ein Koaxialkabel von einem Sender gespeist. Das Kabel ist senkrecht am Haus entlang verlegt und verursacht geringe Störungen. Um das Problem weiter zu verringern, empfiehlt es sich
	beim Koaxialkabel alle 5 m eine Schleife mit 3 Windungen einzulegen.
	das Koaxialkabel durch eine Eindrahtspeiseleitung zu ersetzen.
	den Dipol über ein Symmetrierglied zu speisen.
	das Koaxialkabel in einem Kunststoffrohr zur mechanischen Schirmung unterzubringen.

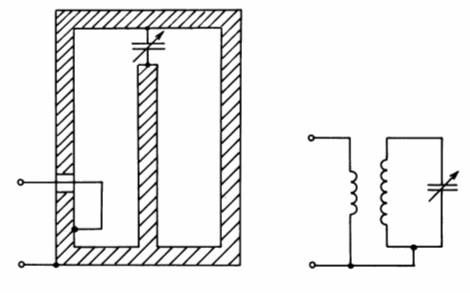
Der Topfkreis

Als Leitungen verwendet man im UHF-Bereich auch Aluminium- oder versilberte Messingbecher mit Mittelleiter, die eine Koaxialleitung darstellen. Man bezeichnet sie als Topfkreise. Topfkreise und auch Paralleldraht-Lecherleitungen lassen sich durch Kurzschlussschieber abstimmen.

Bild 10-19: Topfkreis und Ersatzschaltsymbol

Obiges Bild zeigt einen Parallelschwingkreis mit Drehkondensator in Topfkreistechnik und daneben das herkömmliche Schaltsymbol. Dieser Schwingkreis ist vollkommen abgeschirmt und von außen nicht beeinflussbar. Durch Versilbern der Innenflächen kann man die Verluste sehr gering halten und gute elektrische Eigenschaften für sehr hohe Frequenzen erzielen.

Anhang

Dieser Online-Lehrgang wurde mit freundlicher Genehmigung des Autors aus seinem Buch für das Internet umgewandelt.

Eckart K. W. Moltrecht, "Amateurfunklehrgang für das Amateurfunkzeugnis Klasse 1+2 - TECHNIK" Verlag für Technik und Handwerk, Postfach 2274, 76492 Baden-Baden, 2. Auflage 2007, 309 Seiten, mehr als 300 Abb. ISBN 3-88180-389-0           17,80 €         online bestellen Die 3. Auflage (Klasse A) erscheint im April 2007 *)

Dieser Lehrgang basiert auf dem Prüfungsfragenkatalog Feb. 2007 der Bundesnetzagentur (BNetzA). Alle darin vorkommenden Themen wie Grundlagen der Elektrotechnik, Elektronik sowie Sender- und Empfängertechnik, Übertragungstechnik, Antennentechnik und Messtechnik aus dem Gebiet "Technische Kenntnisse" werden ausführlich erläutert. Die Erfahrung mit praktischen Lehrgängen wird genutzt, um den Prüfling in die Lage zu versetzen, jede Frage aus dem Fragenkatalog richtig zu beantworten. Dieses Buch ist auch sehr gut für das Selbststudium geeignet. Dieser Lehrgang baut auf dem Lehrgang für die Klasse E auf. Sie sollten also erst den Lehrgang für das Amateurfunkzeugnis Klasse E durchgearbeitet haben oder zumindest bei Verweisen dort nachlesen können.

*) Wenn Sie noch vor dem 1. Juni die Prüfung Klasse A (nach dem alten Fragenkatalog Klasse 1+2) machen wollen, sollten Sie sich dieses Buch besorgen, denn es wird in Kürze ausverkauft sein. Bis Ende Mai wird noch nach dem alten Fragenkatalog geprüft.
Dieses Buch online bestellen

Letztes Update: 27.3.2007 (by DJ4UF)