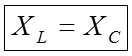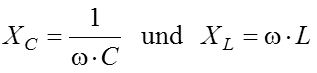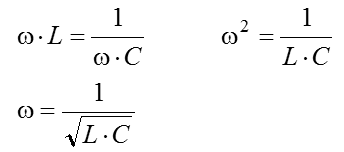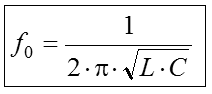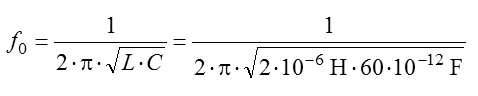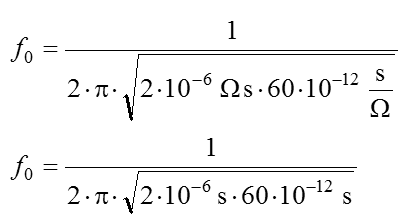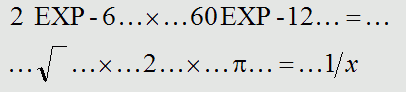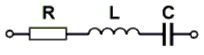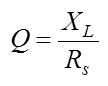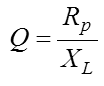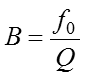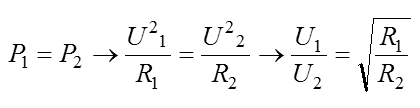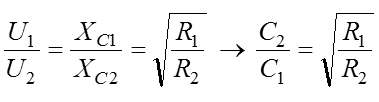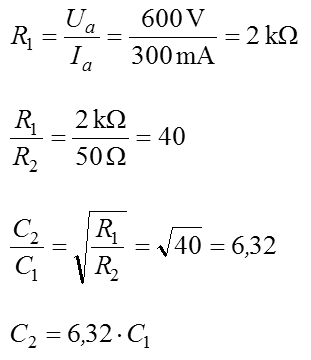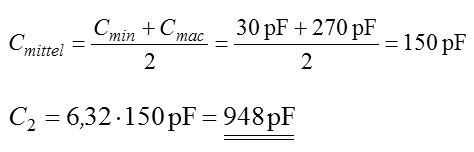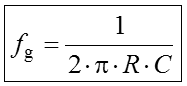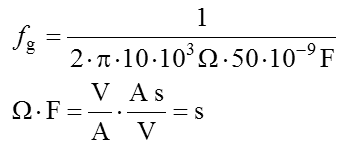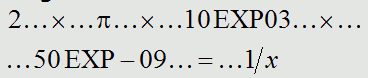Lehrgang nach dem neuen Fragenkatalog vom 28.2.2007

In dieser Lektion werden Prüfungsaufgaben aus dem Sachgebiet Schwingkreis und Filter vorgestellt und ausführlich besprochen. Die Theorie dazu müsste teilweise aus dem Lehrgang für Klasse E bekannt sein.

Übersicht

• Der Schwingkreis
• Die Resonanzfrequenz
• Der Impedanzfrequenzgang
• Die Bandbreite
• Die Güte
• Der Quarz als Schwingkreis
• Bandfilter
• Sperrkreis, Bandpass
• Leitkreis, Saugkreis
• Tiefpass, Hochpass
• Resonanztransformation
• RC-Glieder

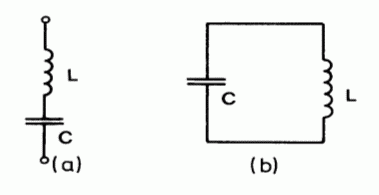
Der Schwingkreis

Sehr ausführlich werden in der Lektion 7 im Amateurfunklehrgang zur Klasse E der Schwingungsvorgang und die Entstehung der sinusförmigen gedämpften und ungedämpften Schwingung erläutert. Beachten Sie bei den Prüfungsaufgaben: Ein Reihenschwingkreis wird auch Serienschwingkreis genannt. Hier werden deshalb beide Begriffe gemischt verwendet.

Bild 4-1: (a) Reihenschwingkreis  oder Serienschwingkreis, (b) Parallelschwingkreis

Die Resonanzfrequenz

Der Begriff Resonanzfrequenz wurde ebenfalls erklärt. Es lief darauf hinaus, dass die Energiependelung bei der Parallelschaltung von Spule und Kondensator am besten bei der Frequenz funktioniert, bei der der induktive Widerstand gleich dem kapazitiven Widerstand ist. Auf eine Ableitung der Formel für die Berechnung der Resonanzfrequenz wurde dort beim Amateurfunklehrgang für die Klasse E verzichtet, was hier nachgeholt werden soll.

Prüfungsfrage

TD203  Was ist im Resonanzfall bei der Reihenschaltung einer Induktivität mit einer Kapazität erfüllt?
	Der Betrag des induktiven Widerstands ist dann gleich dem Betrag des kapazitiven Widerstands.
	Der Wert des Verlustwiderstands der Spule ist dann gleich dem Wert des Verlustwiderstands des Kondensators.
	Die Größe des elektrischen Feldes in der Spule ist dann gleich der Größe des elektrischen Feldes im Kondensators.
	Die Größe des magnetischen Feldes in der Spule ist dann gleich der Größe des magnetischen Feldes im Kondensator.

Aus der Beziehung

lässt sich die Frequenz berechnen, die diese Bedingung erfüllt. Setzt man für

ein und löst man die Gleichung nach ω ω auf, ergibt sich folgender Rechengang.

Nun wird für die Kreisfrequenz ω = 2 π f eingesetzt, dann durch 2π geteilt und man erhält die Frequenz, bei der die Bedingung X_L = X_C erfüllt ist. Diese Frequenz nennt man die Resonanzfrequenz f₀.

Diese Formel – nach dem Ohmschen Gesetz die zweitwichtigste Formel für den Funkamateur – wird als „Thomsonsche Schwing­kreisformel“ bezeichnet. Sie steht auch in der Formelsammlung der BNetzA (siehe Anhang). Dazu gibt es eine Reihe von Prüfungsaufgaben.

Prüfungsfrage

TD209  Welche Resonanzfrequenz hat die Parallelschaltung einer Spule von 2 µH mit einem Kondensator von 60 pF und einem Widerstand von 10 kΩ?
	145,288 kHz
	1,45288 MHz
	14,5288 MHz
	145,288 MHz

Lösung: Bei der Berechnung der Frequenz haben Widerstände keinerlei Wirkung. Warum man noch einen Widerstand angegeben hat, verstehe ich nicht. Vielleicht will man die Aufgabe damit schwieriger machen? Setzen Sie einfach die Kapazität und die Induktivität mit den Einheiten in die Thomsonsche Schwingkreisformel ein.

für H setze ich immer Ωs ein und für F setze ich s/Ω ein. Dann kürzt sich Ohm heraus und es bleibt s² übrig. Daraus die Wurzel ergibt s und 1/s ist Hertz. Sie können aber auch die Grundeinheiten

einsetzen. Dann kürzen sich V und A ebenfalls heraus. Ich kann mir Ohm-Sekunden für Henry einfach besser merken.

Die Thomsonsche Schwingkreisformel gilt auch für die Reihenschaltung von L und C, wie Sie bereits aus dem Lehrgang Klasse E wissen. Lösen Sie also mit dieser Formel nach dem gleichen Prinzip wie bei obiger Aufgabe folgende Prüfungsaufgaben aus dem Fragenkatalog.

Prüfungsfrage

TD207  Wie groß ist die Resonanzfrequenz dieser Schaltung, wenn C1 = 0,1 nF, C2 = 1,5 nF, C3 = 220 pF und L = 1 mH beträgt?
	117,973 kHz
	11,797 kHz
	1,18 kHz
	1,17973 MHz

Prüfungsfrage

TD208  Welche Resonanzfrequenz fres hat die Reihenschaltung einer Spule von 100 µH mit einem Kondensator von 0,01 µF und einem Widerstand von 100 Ω?
	1,59155 kHz
	15,9155 kHz
	159,155 kHz
	1591,55 kHz

Prüfungsfrage

TD210  Wie groß ist die Resonanzfrequenz dieser Schaltung, wenn C = 6,8 pF, R = 10 Ω und L = 1 µH beträgt?
	6,1033 MHz
	61,033 MHz
	610,33 MHz
	610,33 kHz

Prüfungsfrage

TD211  Wie groß ist die Resonanzfrequenz dieser Schaltung, wenn C = 1 nF, R = 0,1 kΩ und L = 10 µH beträgt?
	15,915 kHz
	159,155 kHz
	15,915 MHz
	1,592 MHz

Prüfungsfrage

TD612  Wie verhält sich die Frequenz eines Oszillators bei Temperaturanstieg, wenn die Kapazität des Schwingkreiskondensators mit dem Temperaturanstieg ebenfalls ansteigt?
	Die Frequenz verringert sich.
	Die Schwingungen reißen ab (Aussetzer).
	Die Frequenz erhöht sich.
	Die Frequenz bleibt stabil.

Prüfungsfrage

TD613  Wie verhält sich die Frequenz eines Oszillators bei Temperaturanstieg, wenn die Kapazität des Schwingkreiskondensators mit dem Temperaturanstieg geringer wird?
	Die Frequenz wird niedriger.
	Die Schwingungen reißen ab (Aussetzer).
	Die Frequenz wird erhöht.
	Die Frequenz bleibt stabil.

Prüfungsfrage

TD614  Im VFO eines Senders steigt die Induktivität der Spule mit der Temperatur. Der Kondensator bleibt sehr stabil. Welche Auswirkungen hat dies bei steigender Temperatur?
	Die VFO-Frequenz wandert nach unten.
	Die VFO-Frequenz wandert nach oben.
	Die VFO-Ausgangsspannung nimmt zu.
	Die VFO-Ausgangsspannung nimmt ab.

Zur Thomsonschen Schwingkreisformel gibt es auch noch zwei Fragen ohne Rechnung, nämlich wie sich die Frequenz verändert, wenn man die Induktivität oder die Kapazität erhöht oder erniedrigt. Schauen Sie sich die Formel an: Frequenz und L-C-Produkt sind umgekehrt quadratisch (wegen der Wurzel) proportional. Umgekehrt proportional bedeutet, dass die Frequenz kleiner (geringer) wird, wenn man L oder C erhöht. Quadratisch bedeutet, dass man zum Beispiel C vervierfachen müsste um die halbe Frequenz zu bekommen.

Prüfungsfrage

TD206  Wie ändert sich die Resonanzfrequenz eines Schwingkreises, wenn 1. die Spule mehr Windungen erhält, 2. die Länge der Spule durch Zusammenschieben der Drahtwicklung verringert wird, 3. ein Kupferkern in das Innere der Spule gebracht wird?
	Die Resonanzfrequenz wird bei 1. und 2. kleiner und bei 3. größer.
	Die Resonanzfrequenz wird in allen drei Fällen kleiner.
	Die Resonanzfrequenz wird bei 1. kleiner und bei 2. und 3. größer.
	Die Resonanzfrequenz wird bei 1. und 2. größer und bei 3. kleiner.

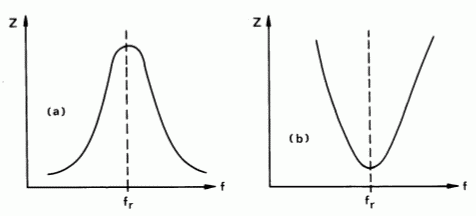
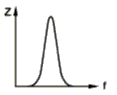
Der Impedanzfrequenzgang

Im Lehrgang zur Klasse E Lektion 7 haben Sie den Scheinwiderstand (Impedanz) eines Parallelschwingkreises aus einer vorgegebenen Messung zeichnen müssen. Für den Reihenschwingkreis (Serienschwingkreis) wurde das Ergebnis vorgegeben. Die Kurven sahen so ähnlich aus, wie in folgendem Bild.

Bild 4-2: Scheinwiderstand
(a) des Parallelschwingkreises und
(b) des Reihenschwingkreises

Aus diesen Kurven kann man folgendes ablesen. Wenn man bei einem Parallel­schwing­kreis die Frequenz langsam erhöht, steigt zunächst der Scheinwiderstand bis zu einem Höchstwert an. Die Frequenz, bei der dieser Höchstwert erreicht wird, heißt Resonanzfrequenz. Der Scheinwiderstand in diesem Punkt heißt Resonanzwiderstand. Erhöht man die Fre­quenz weiter, nimmt der Scheinwiderstand ab.

Prüfungsfrage

TD201  Der Impedanzfrequenzgang in der Abbildung zeigt die Kennlinie
	eines Serienschwingkreises.
	eines Parallelschwingkreises.
	einer Induktivität.
	einer Kapazität.

Prüfungsfrage

TD202  Der im folgenden Bild dargestellte Impedanz-frequenzgang ist typisch für
	einen Serienschwingkreis.
	einen Kondensator.
	eine Spule.
	einen Parallelschwingkreis.

Prüfungsfrage

TD212  Bei Resonanz ist die Impedanz dieser Schaltung ...
	gleich dem reellen Widerstand R.
	unendlich hoch.
	gleich dem kapazitiven Widerstand XC.
	gleich dem induktiven Widerstand XL.

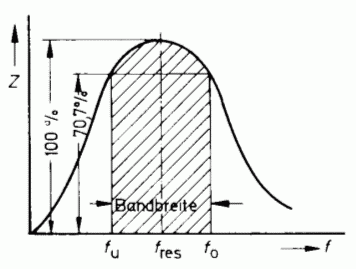
Die Bandbreite

Ein Hochfrequenzverstärker, der mit einem Schwingkreis als Arbeitswiderstand beschaltet ist, verstärkt nicht nur eine einzige Frequenz, sondern einen gewissen Frequenzbereich. Diesen bevorzugten Bereich, bei der die Spannung oder der Schein­widerstand jeweils auf 70,7 Prozent (-3 dB) des Maximalwertes abge­fallen ist, nennt man Bandbreite B.

Bild 4-4: Die Bandbreite eines Parallelschwingkreises

Prüfungsfrage

TD218  Wie ergibt sich die Bandbreite B eines Schwingkreises aus der Resonanzkurve?
	Die Bandbreite ergibt sich aus der Differenz der beiden Frequenzen, bei denen die Spannung auf den 0,7-fachen Wert gegenüber der maximalen Spannung bei der Resonanzfrequenz abgesunken ist.
	Die Bandbreite ergibt sich aus der Differenz der beiden Frequenzen, bei denen die Spannung auf den 0,5-fachen Wert gegenüber der maximalen Spannung bei der Resonanzfrequenz abgesunken ist.
	Die Bandbreite ergibt sich aus der Multiplikation der Resonanzfrequenz mit dem Faktor 0,5.
	Die Bandbreite ergibt sich aus der Multiplikation der Resonanzfrequenz mit dem Faktor 0,7.

Die Güte

Die Bandbreite eines Schwingkreises ist abhängig von der Güte Q des Schwingkreises. Die Güte wiederum ist im Wesentlichen vom Verlustwiderstand der Spule abhängig. Die Verluste des Kondensators sind bei niedrigen und mittleren Frequenzen meistens vernachlässigbar klein. Die Formel für die Güte der Spule finden Sie bereits in der Lektion 3 unter Spule. Sie steht in der Formelsammlung (Anhang) unter Schwingkreis. Wir werden die Formel gleich brauchen und zwar

beim Reihenschwingkreis

und beim Parallelschwingkreis

Wenn Güte Q und Resonanzfrequenz f_res eines Schwingkreises bekannt sind, lässt sich die Bandbreite mit folgender Formel berechnen.

Lösungshinweis: Wenn Sie die Bandbreite bei den anderen angegebenen Frequenzen richtig errechnet haben, muss die Bandbreite bei zunehmender Frequenz proportional größer werden.

Wenn also bei einem Hochfrequenzverstärker eine geringe Bandbreite (hohe Trennschärfe) gewünscht wird, muss entweder die Güte des Schwingkreises hoch sein oder man wählt eine möglichst niedrige Frequenz, zum Beispiel bei der Wahl des Zwischenfrequenzverstärkers eines Empfängers.

Prüfungsfrage

TD215  Welchen Gütefaktor Q hat die Parallelschaltung einer Spule von 2 µH mit einem Kondensator von 60 pF und einem Widerstand von 1 kΩ?
	0,18
	5,5
	18,2
	54,8

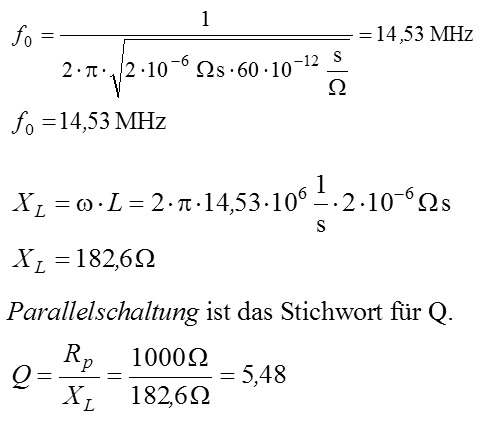
Lösung: Bei dieser Aufgabe ist sicher die Güte bei der Resonanzfrequenz gemeint. Berechnen wir diese zuerst.

Es ist derselbe Wert wie bei TD210.

Die Lösung B ist also die richtige.

Prüfungsfrage

TD214  Welchen Gütefaktor Q hat die Reihenschaltung einer Spule von 100 µH mit einem Kondensator von 0,01 µF und einem Widerstand von 10 Ω?
	10
	1
	0,1
	100

Gleiche Rechnung wie bei der Aufgabe zuvor. Lösung machen?

Prüfungsfrage

TD216  Welche Bandbreite B hat die Reihenschaltung einer Spule von 100 µH mit einem Kondensator von 0,01 µF und einem Widerstand von 10 Ω?
	159 Hz
	1,59 kHz
	15,9 kHz
	159,1 kHz

Lösung: Ansatz

Wir brauchen also die Resonanzfrequenz und die Güte.

Das war eine Menge Rechnerei. Wenn man bedenkt, dass man für eine Aufgabe im Schnitt knapp zwei Minuten Zeit hat (50 Aufgaben in 90 Minuten!), ist das eigentlich nicht zu schaffen. Man muss eine Menge Lösungen mehr oder weniger auswendig können, glaube ich. Aber aufpassen! Bei vielen Aufgaben gibt es mehrere ähnliche Aufgaben mit verwechselbaren Lösungen.

Prüfungsfrage

TD217  Welche Bandbreite B hat die Parallelschaltung einer Spule von 2 µH mit einem Kondensator von 60 pF und einem Widerstand von 1 kΩ?
	26,5 MHz
	2,65 MHz
	795,8 kHz
	79,6 kHz

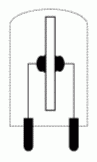
Der Quarz als Schwingkreis

Ein ähnliches Verhalten wie ein LC-Schwingkreis aus Kondensator und Spule hat ein Schwingquarz.

  Bild 4-5: Ein Quarz

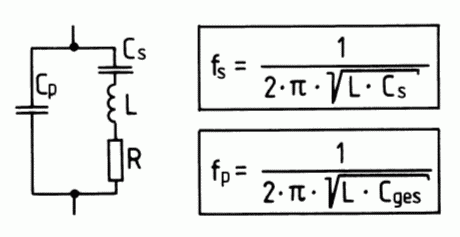
Dieser besteht aus sehr reinem Siliziumdioxid und wird als dünnes Plättchen aus einem Quarzkristall herausgeschnitten. Sein Verhalten ist durch den umkehrbaren piezoelektrischen Effekt gekennzeichnet. Unter dem piezoelektrischen Effekt versteht man die Erscheinung, dass zwischen zwei Seiten eines Kristalls bei Druck- oder Zugbeanspruchung elektrische Spannung entsteht. Eine Anwendung dieser Erscheinung findet man bei Gasanzündern oder Feuerzeugen.

Beim Quarz ist dieser Effekt umkehrbar, das heißt bei Anlegen einer Spannung verbiegt sich das Quarzplättchen (Biegeschwinger) oder verändert seine Dicke (Dickenschwinger). Durch Verbiegen entsteht wieder eine Spannung, die ihrerseits wieder eine Verbiegung bewirkt und so weiter.

Durch die Laufzeit der Druckwelle ist dieser Effekt von der Dicke des Quarzplättchens abhängig. Je dünner das Plättchen ist, desto schneller schwingt der Quarz, desto höher ist also die Frequenz. Herstellbar sind Grundwellenquarze für Frequenzen von 50 kHz bis etwa 15 MHz.

Die Dämpfung dieser Schwingung ist gering, so dass praktisch ein Schwingkreis hoher Güte entsteht. Für einen Schwingquarz kann man in der Nähe seiner Reso­nanz folgende Ersatzschaltung angeben.

Bild 4-6: Der Quarz als Schwingkreis

Aus der Ersatzschaltung geht hervor, dass der Schwingkreis zwei Resonanzstellen haben muss. C_S, L (und R) stellen einen Serienkreis dar. Dies nennt man die Serien­resonanzfrequenz f_S. Ferner kann man sich die beiden Kondensatoren C_S und C_P innerhalb des Schwingkreises als in Reihe geschaltete Kondensatoren denken, die dann zur Spule mit dem Verlustwiderstand parallel liegen und eine etwas höhere Resonanzfrequenz ergeben, die Parallelresonanz f_P.

Bild 4-7: Der Quarz als Schwingkreis

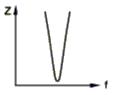
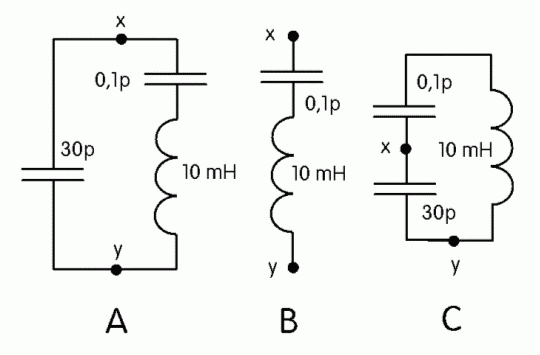
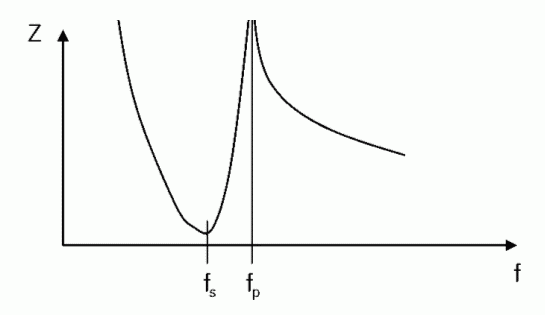
Für Interessierte: Es soll hier an einem Beispiel mathematisch nachgewiesen werden, dass die Serienresonanz- und die Parallelresonanzfrequenz dicht nebeneinander liegen. Dazu wurde das Ersatzbild des Quarzes für die beiden Fälle ein wenig umgezeichnet und vereinfacht (ohne R).

Im Bild 4-7 A ist das vereinfachte Ersatzbild eines Quarzes dargestellt. Typische Werte für die Serien- und die Parallelkapazität sowie die Induktivität sind angegeben. Verfolgt man den Weg auf der rechten Seite von x nach y erhält man den Serienschwingkreis nach Bild B. Mit diesen Werten ergibt sich eine Serienresonanzfrequenz (rechnen Sie nach!) von 5,035 MHz.

Geht man von der Spule aus, liegen die beiden Kondensatoren als Reihenschaltung parallel dazu (Bild 4-6a C). Die Reihenschaltung der C’s ergibt 0,099668 pF. Damit ergibt sich eine Parallelresonanzfrequenz von 5,041 MHz.

Zeichnet man den Impedanzverlauf des Quarzes auf, erhält man prinzipiell folgendes Bild.

Bild 4-8: Impedanzverlauf Quarz als Schwingkreis

Bei der Serienresonanzfrequenz hat der Quarz einen sehr geringen, bei der Parallelresonanz einen sehr hohen Widerstand. Prüfungsfragen dazu gibt es bei Oszillatoren (Siehe Lektion 7, Bild 7-10).

Quarze werden für Generatoren (Oszillatoren) im Hochfrequenzbereich angewendet, die eine sehr konstante Frequenz haben sollen. Man erreicht Genauigkeiten von 10^-6 (1 ppm) bis 10^-8 (0,01 ppm), das heißt Abweichungen von einem Millionstel bis sogar ein Hundertstel von einem Millionstel. Siehe Prüfungsaufgabe TA117.

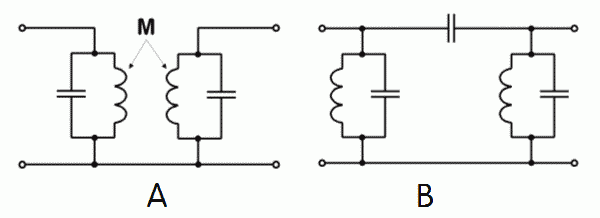
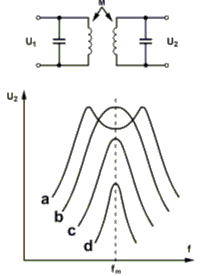
Bandfilter

Koppelt man zwei oder mehr Parallelschwingkreise in bestimmter Weise, nennt man die entstehende Schaltung Bandfilter. Die Schaltung heißt deshalb Bandfilter, weil sie ein bestimmtes Frequenzband (Frequenzbereich) durchlässt und die anderen Frequenzen sperrt.

 

Bild 4-9: Kopplungsarten bei Bandfiltern
A: Induktive Kopplung, B: Kapazitive Kopplung

Je nachdem, wie fest man die Schwingkreise miteinander koppelt, entstehen unterschied­liche Bandbreiten des Bandfilters.

Bild 4-10: Kopplungsarten: a) unterkritische,
b) kritische, c) überkritische Kopplung

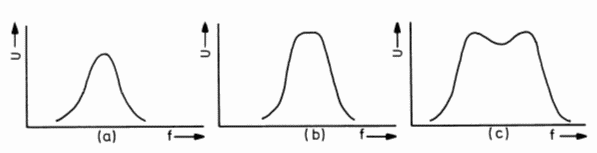
Bei fester Kopplung (überkritische Kopplung) entsteht eine Einsattelung der Resonanzkurve (Bild 4-10 c). Bei der kritischen Kopplung hat die Kurve ein waagerechtes Dach (flat top) und bei unterkritischer Kopplung oder loser Kopplung erhält man die Resonanzkurve wie bei einem Einzelkreis (Bild 4-10 a) und die übertragene Spannung wird geringer.

Prüfungsfrage

TD228  Welche Kopplung eines Bandfilters wird "kritische Kopplung" genannt?
	Die Kopplung, bei der die Resonanzkurve des Bandfilters eine Welligkeit von 3 dB (Höcker- zu Sattelspannung) zeigt.
	Die Kopplung, bei der die Resonanzkurve des Bandfilters ihre größtmögliche Breite hat.
	Die Kopplung, bei der die Resonanzkurve ihre größte Breite hat und dabei am Resonanzmaximum noch völlig eben ist.
	Die Kopplung, bei der die Ausgangspannung des Bandfilters das 0,707-fache der Eingangsspannung erreicht.

Prüfungsfrage

TD224  Welche der nachfolgenden Beschreibungen trifft auf diese Schaltung zu und wie nennt man sie?
	Es handelt sich um eine Bandsperre. Frequenzen oberhalb der oberen Grenzfrequenz und Frequenzen unterhalb der unteren Grenzfrequenz werden durchgelassen. Sie bedämpft nur einen bestimmten Frequenzbereich.
	Es handelt sich um einen Hochpass. Frequenzen unterhalb der Grenzfrequenz werden bedämpft, oberhalb der Grenzfrequenz durchgelassen.
	Es handelt sich um einen Tiefpass. Frequenzen oberhalb der Grenzfrequenz werden bedämpft, unterhalb der Grenzfrequenz durchgelassen.
	Es handelt sich um einen Bandpass. Frequenzen oberhalb der oberen Grenzfrequenz und Frequenzen unterhalb der unteren Grenzfrequenz werden bedämpft. Er lässt nur einen bestimmten Frequenzbereich passieren.

Prüfungsfrage

TD229 Das folgende Bild zeigt ein induktiv gekoppeltes Bandfilter und vier seiner möglichen Übertragungskurven (a bis d). Welche der folgenden Aussagen ist richtig?
	Bei der c-Kurve ist die Kopplung loser als bei der a-Kurve.
	Bei der b-Kurve ist die Kopplung loser als bei der c-Kurve.
	Bei der a-Kurve ist die Kopplung loser als bei der c-Kurve.
	Bei der b-Kurve ist die Kopplung loser als bei der d-Kurve.

Hinweis: Siehe Bild 4-10!

Prüfungsfrage

TD230 Das folgende Bild zeigt ein typisches ZF-Filter und vier seiner möglichen Übertragungskurven (a bis d). Welche Kurve ergibt sich bei kritischer Kopplung und welche bei überkritischer Kopplung?
	Die c-Kurve zeigt kritische, die b-Kurve zeigt überkritische Kopplung.
	Die a-Kurve zeigt kritische, die b-Kurve zeigt überkritische Kopplung.
	Die b-Kurve zeigt kritische, die a-Kurve zeigt überkritische Kopplung.
	Die d-Kurve zeigt kritische, die c-Kurve zeigt überkritische Kopplung.

Hinweis: Siehe Bild 4-10! Kritisch: Es wird das Maximum erreicht. Überkritisch: Es wird das Maximum "überschritten", d.h. es gibt einen Einbruch.

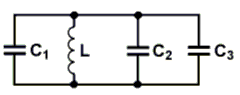
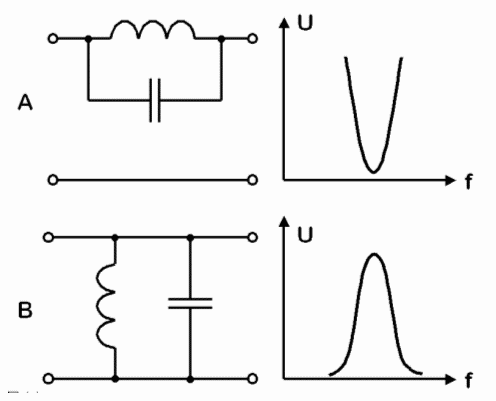
Sperrkreis, Bandpass, Leitkreis, Saugkreis

Den Parallelschwingkreis und den Serienschwingkreis kann man außer in Bandfilterkombinationen auch in Leitungswege einschleifen und erhält damit verschiedene Anwendungen.

Bild 4-11: A Sperrkreis, B Bandpass

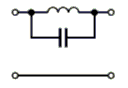
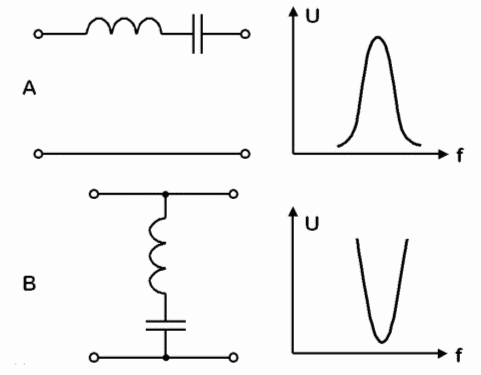
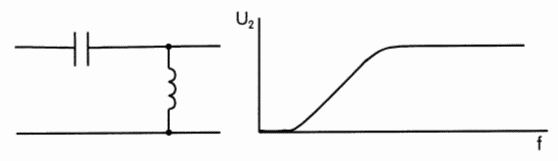
Schaltet man wie in Bild 4-11 A einen Parallelkreis in Reihe zum Signalweg, erhält man einen „Sperrkreis“ oder auch Sperrfilter, denn für den Bereich um die Resonanzfrequenz mit entsprechender Bandbreite ist der Scheinwiderstand groß. Dadurch wird dieser Bereich gesperrt. Achten Sie beim Frequenzgang darauf, dass hier die Spannung am Ausgang aufgetragen ist und nicht wie bei den Prüfungsfragen TD201 bis TD203 die Impedanz!

Schaltet man den Parallelschwingkreis parallel zum Signalweg, werden alle Frequenzen neben der Resonanzfrequenz kurzgeschlossen. Es bleibt nur noch ein schmaler Bandbereich übrig. Man erhält einen Bandpass.

Prüfungsfrage

TD222  Was stellt diese Schaltung dar?
	Sperrkreis
	Hochpass
	Saugkreis
	Tiefpass

Prüfungsfrage

TD223  Bei dem dargestellten Filter handelt es sich um ein ...
	Dämpfungsglied.
	Tiefpassfilter.
	Hochpassfilter.
	Sperrfilter.

Bild 4-12: A Leitkreis, B Saugkreis

Mit Serienschwingkreisen kann man ein ähnliches Verhalten erzielen. Schaltet man einen Reihenschwingkreis in Reihe zum Signalweg, werden bevorzugt die Frequenzen durchgelassen, die in dem Bereich der Bandbreite des Schwingkreises liegen, weil er dort sehr niederohmig ist und die Signale gut durchlässt. Man nennt ihn Leitkreis, also einen Schwingkreis der gut leitet.

Prüfungsfrage

TF320 TF319 Welche Konfigurationen wäre für die Unterdrückung unerwünschter Signale am Eingang eines Empfängers hilfreich?

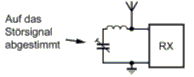
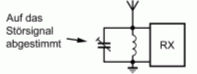
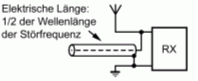
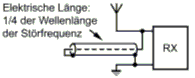
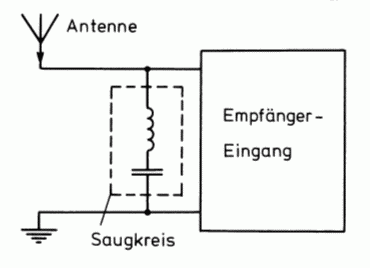
Die Besprechung der Schaltungen C und D erfolgt später.

Ein umgekehrtes Verhalten bekommt man, wenn der Serienschwingkreis zum Signalweg parallel geschaltet wird wie im Bild 4-12 B. Bei der Resonanzfrequenz leitet der Kreis sehr gut und schließt diese Frequenzen praktisch kurz. Man nennt die Schaltung Saugkreis, weil sie einen schmalen Frequenzbereich „absaugt“. Ein Anwendungsbeispiel wurde weiter oben im Bild 4-3 gezeigt.

Ein Reihenschwingkreis stellt wegen der Eigenschaft, dass er bei einer Frequenz (Resonanzfrequenz) praktisch einen Kurzschluss darstellt, einen Saugkreis dar. Er wird zum Beispiel zur Störungsunterdrückung beim gestörten Empfänger eingesetzt.

Bild 4-3: Anwendung des Reihenschwingkreises als Saugkreis

 

Prüfungsfrage

TD221  Was stellt diese Schaltung dar?
	Sperrkreis
	Hochpass
	Saugkreis
	Tiefpass

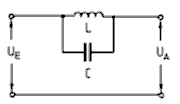
Tiefpass – Hochpass

Bild 4-13: Der Tiefpass (links) und der zugehörige Frequenzgang (rechts)

Andere Kombinationen von Spule und Kondensator stellen folgende Schaltungen dar. Diese wurden bereits im Lehrgang zur Klasse E vorgestellt und erläutert.

Prüfungsfrage

TD220  Was stellt diese Schaltung dar?
	Hochpass
	Tiefpass
	Saugkreis
	Sperrkreis

Bild 4-14: Der Hochpass (links) und der zugehörige Frequenzgang

Prüfungsfrage

TD219  Was stellt diese Schaltung dar?
	Hochpass
	Bandpass
	Sperrkreis
	Tiefpass

Bild 4-15: Tiefpass in T-Schaltung (A) und in Pi-Schaltung (B)

Prüfungsfrage

TD226  Welche Schaltung stellt ein Hochpassfilter dar?

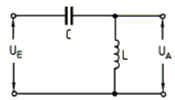
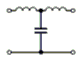
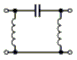
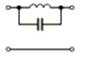
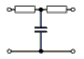
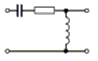
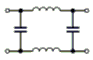
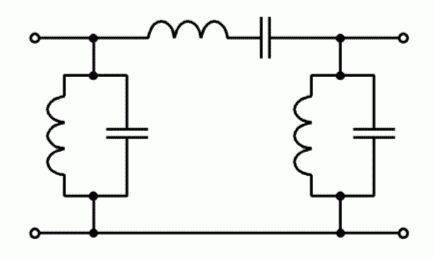
Das Tiefpassfilter in Pi-Schaltung nach Bild 4-15 B lässt sich gut als Entstörfilter für die Netzleitung verwenden. Die tiefe Frequenz von 50 Hertz wird gut durchgelassen aber die höheren Funkfrequenzen werden unterdrückt und gelangen nicht in die Netzleitung. Allerdings wird dieses Filter meisten symmetrisch aufgebaut, damit beide Netzleitungen entstört werden. Sie finden die Schaltung in folgender Prüfungsaufgabe.

Prüfungsfrage

TB214 TD322  Welche der dargestellten Schaltungen könnte in den Netzeingang eines Geräts eingebaut werden, um HF-Rückfluss in das Stromversorgungsnetz zu verringern?

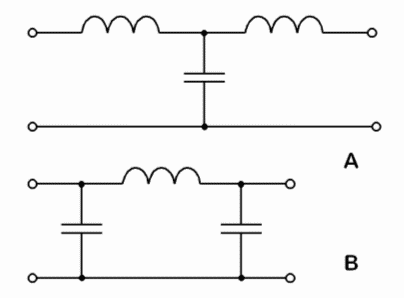
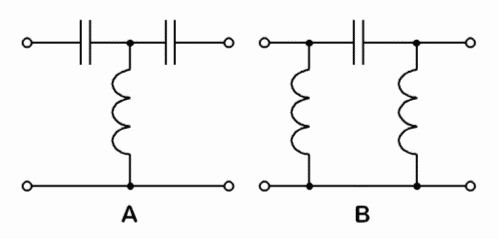
Kommentar: Es soll keine Gleichstromleistung verloren gehen, aber hohe Frequenzen unterdrückt werden.

Es lassen sich mehrere Tiefpass- oder Hochpassglieder hintereinander schal­ten. Bei einer Hintereinanderschaltung von zwei Tiefpassgliedern unterscheidet man die T-Schaltung (Bild 4-14 A) weil sie wie ein großes „T“ aussieht und die Pi-Schaltung, weil sie wie ein griechischer Buchstabe  aussieht. Gleiches gilt für entsprechende Hochpassschaltungen, wenn man Spulen und Kondensatoren miteinander vertauscht.

Bild 4-16: Hochpass in T-Schaltung (A) und in Pi-Schaltung (B)

Prüfungsfrage

TD225  Im folgenden Bild ist ein Filter dargestellt. Es handelt sich um
	ein Tiefpassfilter.
	ein Sperrfilter.
	ein Notchfilter in Verbindung mit einem Hochpassfilter.
	ein Hochpassfilter.

 

Bild 4-17: Bandpass

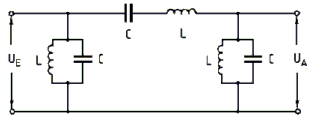
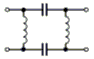
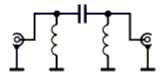
Im Bild 4-17 handelt es sich um die Kombination aus der Parallelschaltung von Parallelschwingkreisen und der Serienschaltung eines Serienschwingkreises. Man erreicht steilere Filterflanken. Dadurch wird die Durchlasswirkung verbessert.

In der Sendertechnik - besonders bei Röhrenendstufen - wird ein spezielles Pi-Filter für die Anpassung des Senderinnen­widerstandes an die Antenneneingangs­impedanz verwendet.

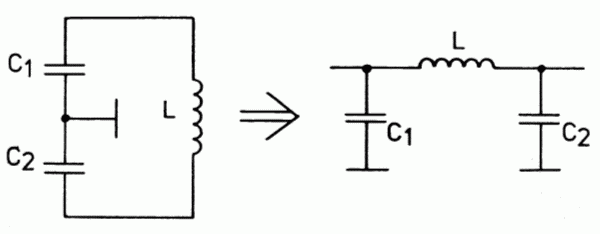
Resonanztransformation

Schwingkreise in Resonanz kann man sehr gut für Transformationszwecke verwenden. Dabei wird nicht die Induktivität als Transformator verwendet sondern das Verhältnis der Kapazitäten von zwei in Reihe geschalteten Kondensatoren. Als Kondensatoren verwendet man oft veränderbare Drehkondensatoren und kann so stufenlos anpassen.

Bild 4-18: Collinsfilter oder Pi-Filter

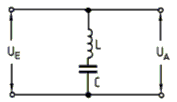
Im Bild sieht man links den normalen Schwingkreis mit zwei in Reihe geschal­teten Kondensatoren, zwischen denen der Massepunkt liegt. Etwas umgezeichnet wird daraus die Pi-Schaltung. Für Interessierte folgt eine Ableitung einer Formel, wie man mit dem Verhältnis der Kondensatoren die Widerstände anpassen kann. Nehmen wir an, der Ausgang wird mit R₂ belastet. Dies ist kein Prüfungsthema!

Eingangsleistung gleich Ausgangsleistung:

Außerdem verhalten sich in einem abgestimmten Schwingkreis die Spannungen wie die Wechselstromwiderstände.

Die Kapazitäten verhalten sich also umgekehrt wie die zu transformierenden Widerstände.

Lösung: Der Röhreninnenwiderstand R₁ berechnet sich aus dem Verhältnis von Anodenspannung zu Anodenstrom.

Der antennenseitige Kondensator müsste also 6,32-mal größer sein als der Mittelwert des anodenseitigen Drehkos. Der Mittelwert des Drehkos C₁ ist

 Prüfungsfrage

TG315  Das folgende Bild zeigt eine HF-Endstufe. Welche Bedeutung und Funktion haben C1, C2 und L1?  Wie sind die Bedienknöpfe der beiden Kondensatoren an einer Endstufe wahrscheinlich beschriftet?
	An dem Drehknopf für C1 steht "CPlate" oder "Plate", an dem für C2 steht "CLoad" oder "Load". Die drei Bauelemente C1, C2 und L1 bilden zusammen einen so genannten Pi-Tankkreis zur Anpassung der Ausgangsimpedanz der Röhre an die Antennenimpedanz.
	An dem Drehknopf für C1 steht "CLoad" oder "Load", an dem für C2 steht "CPlate" oder "Plate". Die drei Bauelemente C1, C2 und L1 bilden zusammen ein abstimmbaren Sperrkreis zur Unterdrückung von Harmonischen.
	An dem Drehknopf für C1 steht "CPlate" oder "Plate", an dem für C2 steht "CLoad" oder "Load". Die drei Bauelemente C1, C2 und L1 bilden zusammen ein abstimmbaren Sperrkreis zur Unterdrückung von Harmonischen.
	An dem Drehknopf für C1 steht "CLoad" oder "Load", an dem für C2 steht "CPlate" oder "Plate". Die drei Bauelemente C1, C2 und L1 bilden zusammen einen so genannten Pi-Tankkreis zur Anpassung der Ausgangsimpedanz der Röhre an die Antennenimpedanz.

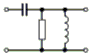
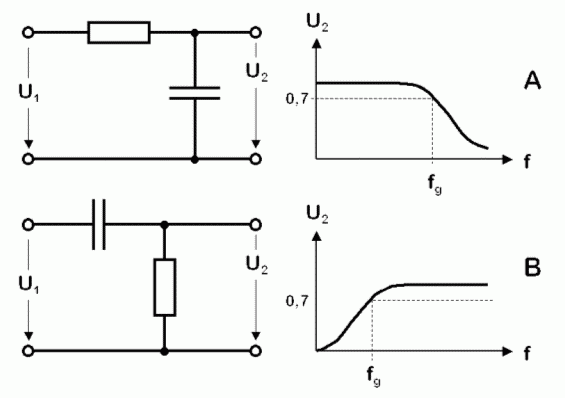
RC-Glieder als Tief- und Hochpass

Anstatt Spule lässt sich auch ein billiger Widerstand einsetzen. Das Verhalten bleibt prinzipiell gleich. Jedoch sind die Flanken weniger steil.

Bild 4-19: RC-Glieder A: Tiefpass, B: Hochpass

Die Frequenz, bei der beim Tiefpass die Ausgangsspannung auf 70,7% (-3dB) abgesunken beziehungsweise beim Hochpass 70,7% des Endwertes erreicht wird, nennt man Grenzfrequenz. Die Grenzfrequenz f_g dieser RC-Glieder lässt sich recht einfach berechnen. Die Formel steht in der Formel­sammlung der BNetzA (Anhang).

 Prüfungsfrage

TD213  Welche Grenzfrequenz ergibt sich bei einem RC-Tiefpass mit einem Widerstand von 10 kΩ und einem Kondensator von 50 nF?
	0,32 Hz
	318 Hz
	421 Hz
	318 kHz

Lösung:

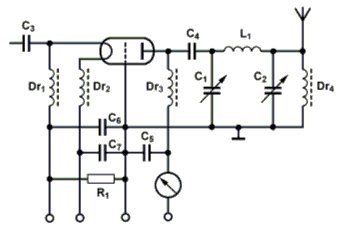
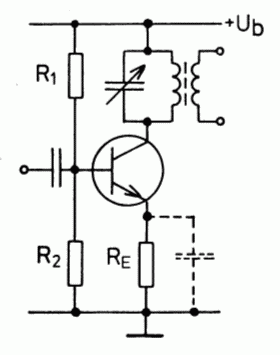
Und so sieht eine Anwendung des Parallelschwingkreises bei einem Hochfrequenzverstärker aus. Die Wicklung des Übertragers dient als Schwingkreisinduktivität. Mehr dazu in Lektion 7!

Anhang

Dieser Online-Lehrgang wurde mit freundlicher Genehmigung des Autors aus seinem Buch für das Internet umgewandelt.

Eckart K. W. Moltrecht, "Amateurfunklehrgang für das Amateurfunkzeugnis Klasse 1+2 - TECHNIK" Verlag für Technik und Handwerk, Postfach 2274, 76492 Baden-Baden, 2. Auflage 2007, 309 Seiten, mehr als 300 Abb. ISBN 3-88180-389-0                17,80 € Die 3. Auflage (Klasse A) erscheint im April 2007 *)

Dieser Lehrgang basiert auf dem Prüfungsfragenkatalog Feb. 2007 der Bundesnetzagentur (BNetzA). Alle darin vorkommenden Themen wie Grundlagen der Elektrotechnik, Elektronik sowie Sender- und Empfängertechnik, Übertragungstechnik, Antennentechnik und Messtechnik aus dem Gebiet "Technische Kenntnisse" werden ausführlich erläutert. Die Erfahrung mit praktischen Lehrgängen wird genutzt, um den Prüfling in die Lage zu versetzen, jede Frage aus dem Fragenkatalog richtig zu beantworten. Dieses Buch ist auch sehr gut für das Selbststudium geeignet. Dieser Lehrgang baut auf dem Lehrgang für die Klasse E auf. Sie sollten also erst den Lehrgang für das Amateurfunkzeugnis Klasse E durchgearbeitet haben oder zumindest bei Verweisen dort nachlesen können.

*) Wenn Sie noch im vor dem 1. Juni die Prüfung Klasse A (nach dem alten Fragenkatalog Klasse 1+2) machen wollen, sollten Sie sich dieses Buch besorgen, denn es wird in Kürze ausverkauft sein. Bis Ende Mai wird noch nach altem Fragenkatalog geprüft.
Dieses Buch online bestellen ...

---

Letztes Update: 17.3.2007 (by DJ4UF)