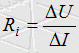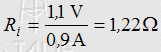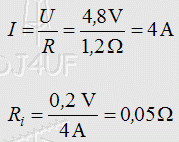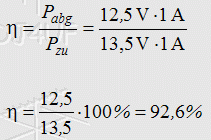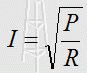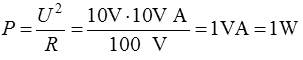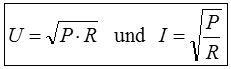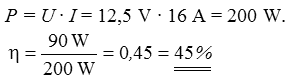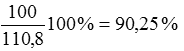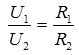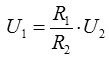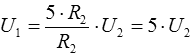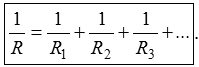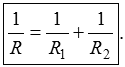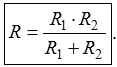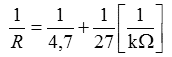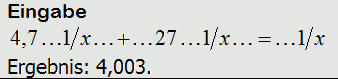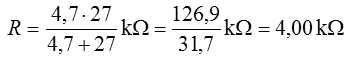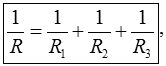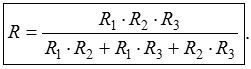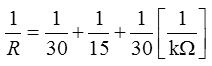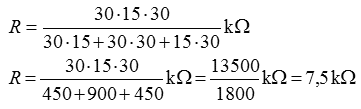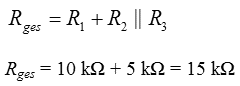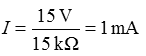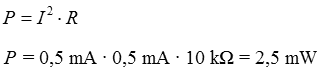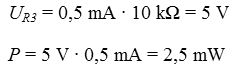|
|
Amateurfunklehrgang Klasse A von E. Moltrecht, DJ4UF |
Lehrgang nach dem neuen Fragenkatalog vom 28.2.2007
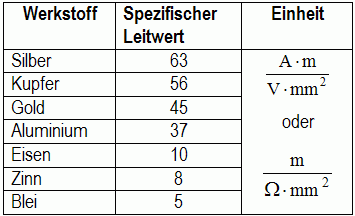
Lektion 2: Der Widerstand und seine GrundschaltungenIn dieser Lektion werden Prüfungsaufgaben aus folgenden Gebieten vorgestellt und ausführlich besprochen. Die Theorie dazu müsste aus dem Lehrgang für Klasse E bekannt sein. Jedoch werden für Klasse A mehr Berechnungen verlangt. Übersicht Die elektrische Leitfähigkeit Verschiedene Materialien leiten den Strom unterschiedlich gut. Zur Leitfähigkeit finden Sie im Lehrgang zur Klasse E in der Lektion 4 ein Kapitel Spezifischer Widerstand - Spezifischer Leitwert mit folgender Tabelle.
Prüfungsfrage
Zur Lösung: Es sind Stoffe wie zum Beispiel Silizium oder Germanium, die in reinem Zustand nicht leiten (also gute Isolatoren sind) und durch Hinzugabe von geeigneten Zusätzen eine gewisse Leitfähigkeit bekommen, die aber nicht so hoch ist wie die Leitfähigkeit der Metalle. Deshalb der Name Halbleiter! Die Halbleiter werden in der Lektion 5 dieses Buches ausführlich behandelt. Prüfungsfrage:
Zur Lösung: Nichtleiter oder Isolatoren sind Glas, Porzellan, Kunststoffe, trockenes Papier und Holz. In der Zeile a stehen nur Kunststoffe (Lösung), während in den anderen Zeilen mit Graphit (Kohlenstoff), Messing oder Bronze auch mindestens ein Leiter vorkommt und damit diese Lösungen ausscheiden. Der LeiterwiderstandPrüfungsfrage:
Zur Lösung: Metallische Leiter enthalten sehr viele freie Elektronen. Durch Wärme werden diese Elektronen in ihrer geradlinigen Bewegung gestört. Wegen dieser schlechteren Beweglichkeit behindern sie sich gegenseitig und der Widerstand erhöht sich. Lösung D ist richtig. Mit Hilfe des spezifischen Widerstandes kann man den Widerstand eines Leiters berechnen. Folgende Formel finden Sie im Anhang (Formelsammlung der BNetzA). Der spezifische Widerstand ρ (rho) ist der Kehrwert des spezifischen Leitwerts und wird angegeben als der Widerstand in Ohm bei 1 m Länge und 1 mm2 Querschnitt. Prüfungsfrage:
Lösungshinweis: 1 m sind 1000 mm.
Bei der folgenden Prüfungsfrage ist Mathematik gefragt. Sie brauchen außer der Formel für den Widerstand auch noch die Formel zur Berechnung der Querschnittsfläche eines kreisförmigen Leiters. Wenn Ihnen diese Mathematik nicht liegt, müssen Sie sich das sehr einfache Ergebnis merken, denn die Prüfungsfrage wird immer mit diesen Werten gestellt. Prüfungsfrage:
Zur Lösung: Jetzt muss gerechnet werden! Zunächst muss die Querschnittsfläche des Leiters berechnet werden, da nur der Durchmesser angegeben ist. Die Formel für die Kreisfläche lautet (Siehe Formelsammlung!). Der spezifische Widerstand für Kupfer steht in der bei der Prüfung zur Verfügung gestellten Formelsammlung der BNetzA mit Prüfungsfrage:
Lösung: Wir benutzen wieder folgende Formel aus der Formelsammlung. Die Formel muss nach der Länge l umgestellt werden. Der Skin-Effekt Jeder Strom durchflossene Leiter erzeugt ein Magnetfeld. Dieses Magnetfeld verläuft auch im Innern eines Kupferleiters. Durch das Magnetfeld werden besonders bei hohen Frequenzen die Elektronen aus der Mitte des Leiters zusammen gedrängt. Es wirkt sich so aus, als ob die Querschnittsfläche für den Stromfluss geringer wird. Bei Frequenzen ab zirka 10 MHz wirkt sich dieser Effekt so stark aus, dass die Elektronen praktisch nur noch an der Oberfläche (englisch: skin) des Leiters fließen. Um die Leitfähigkeit zu verbessern, versilbert man die Oberfläche des Leiters. Oder man stellt den Leiter für Hochfrequenz aus vielen voneinander isolierten dünnen Drähten her, die in mehreren Stufen miteinander verdrillt werden. Besonders für Antennendrähte und für Hochfrequenzspulen werden solche Drähte verwendet. Prüfungsfrage:
Prüfungsfrage:
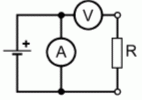
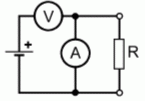
Ohmsches Gesetz, Leistung Um einen Widerstand berechnen zu können, benötigt man die Spannung am Widerstand und den Strom durch den Widerstand. Dann gilt nach dem ohmschen Gesetz
Eselsbrücken: Sie kennen R-u-d-i? R = U durch I oder den Schweizer Kanton URI? Schauen Sie auch in der Lektion 1 nach dem URI-Dreieck! Allerdings gilt dieser einfache Zusammenhang nur, wenn Strom und Spannung in Phase sind. Wenn Kondensatoren oder Spulen in der Schaltung enthalten sind, treten Phasenverschiebungen zwischen Spannung und Strom auf. Die Berechnung muss dann den Phasenwinkel berücksichtigen. Man nennt es auch eine "geometrische" Berechnung oder Rechnungen mit "Vektoren". Diese kommen in der Prüfung für das Amateurfunkzeugnis nicht vor. Prüfungsfrage
ToleranzIn der Lektion 4 Im Buch zur Klasse E wird das Toleranzschema ausführlich dargestellt. In der Prüfung Klasse A gibt es dazu nur eine Prüfungsfrage. Prüfungsfrage
Lösung machen? 0,1 mal 5600 sind 560 .... Aufbau von Widerständen Beim Aufbau von Widerständen unterscheidet man Kohleschichtwiderstände, Metallschichtwiderstände, Metalloxidwiderstände und Drahtwiderstände. Im Amateurfunklehrgang zur Klasse E, Lektion 4 sind die Eigenschaften genauer beschrieben. Zusammenfassung: Kohleschichtwiderstände sind billig, haben aber eine relativ große Herstellungstoleranz. Metallschichtwiderstände sind Präzisionswiderstände. Metalloxidwiderstände eignen sich besonders für Hochfrequenz. Drahtwiderstände eignen sich als Hochlastwiderstände bei niedrigen Frequenzen (Niederfrequenzbereich). Prüfungsfrage
Prüfungsfrage
Prüfungsfrage
Prüfungsfrage
Kommentar: Drahtwiderstände wirken durch den aufgewickelten Draht wie Spulen und sind deshalb nicht für hohe Frequenzen geeignet.
Prüfungsfrage:
Kommentar: Schichtwiderstände sind geeignet, vor allem dann, wenn sie nicht gewendelt sind. Hochohmige Widerstände vergrößert man in ihrem Widerstandswert, indem man eine Wendel einschleift. Dann werden sie aber wieder induktiv.
Prüfungsfrage:
Kommentar: Man kann Schichtwiderstände parallel schalten, um die leistungsaufnahme zu erhöhen. 10 Stück zu 500 Ohm parallel ergeben 50 Ohm, die übliche Antennenimpedanz.
Prüfungsfrage:
Kommentar: Schichtwiderstände sind geeignet, vor allem dann, wenn sie nicht gewendelt sind. Hochohmige Widerstände vergrößert man in ihrem Widerstandswert, indem man eine Wendel einschleift. Dann werden sie aber wieder induktiv. Der Innenwiderstand Für Netzteile zur Spannungsversorgung von Geräten benutzt man Spannungsquellen, die einen sehr geringen Innenwiderstand haben sollen, damit die Spannung konstant bleibt. Zum Laden von Akkus wird gelegentlich eine Stromquelle gebraucht, bei der der Strom konstant bleiben soll. Dies geht nur bei großem Innenwiderstand oder besser ausgedrückt, wenn der Innenwiderstand der Spannungsquelle viel größer ist als der Lastwiderstand. In diesem Zusammenhang folgen einige Aufgaben zum Thema Leistungsanpassung, Stromanpassung, Spannungsanpassung. Prüfungsfrage:
Kommentar: Siehe Absatz oberhalb!
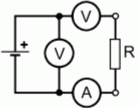
Prüfungsfrage:
Lösungsweg: Durch den Innenwiderstand fällt bei einer Spannungsquelle immer etwas Spannung ab, wenn Strom fließt. Dieser Spannungsabfall berechnet sich nach dem ohmschen Gesetz zu
wobei ΔU der Spannungsabfall ist und ΔI die Stromänderung. Um den Innenwiderstand zu berechnen, kann man diese Formel nach Ri umstellen. Der Spannungsunterschied ist in diesem Fall 13,5 V - 12,4 V = 1,1 V und der Stromunterschied von Null bis 0,9 A also 0,9 A. Diese Werte werden in die Formel eingesetzt. Prüfungsfrage:
Lösung machen? Echt? 0,5 V geteilt durch 2 A =?
Prüfungsfrage:+
Lösungsweg: Auch hier rechnen wir mit der Formel Spannungsänderung durch Stromänderung. Der Strom muss allerdings vorher ausgerechnet werden. Sie müssen bei der Berechnung des Stroms berücksichtigen, dass dann nur noch 4,8 Volt vorhanden sind. Rechnen Sie also nicht mit der Leerlaufspannung den Strom aus! Prüfungsfrage:
Lösungsweg: Unter Wirkungsgrad versteht man das Verhältnis von der abgegebenen Leistung zur "aufgewendeten" Leistung. Die Spannungsquelle erzeugt 13,5 Volt und liefert dabei 1 Ampere. An den Ausgangsklemmen kommen nur noch 12,5 Volt an. Der Rest erzeugt Wärme am Innenwiderstand. Damit berechnet sich der Wirkungsgrad zu Prüfungsfrage
Lösung machen? Ansonsten siehe TB204!
Prüfungsfrage
Kommentar: Leistungsanpassung ist die Anpassung in der Nachrichtentechnik. Da müssen alle Widerstände (Impedanzen) zueinander passen, also R1 = R2, oder RL = Ri.
Prüfungsfrage
Spannungsanpassung findet beim normalen Netzteil statt. Es soll keine Spannung verloren gehen. Also muss der Innenwiderstand (Ri) klein sein. Tipp für sehr viel "kleiner": Die kleinen Spitzen zeigen auf die Größe Ri. Prüfungsfrage
Für Stromanpassung bleibt dann der große Innenwiderstand. Groß steht dann für die Seite, an der die spitzen Pfeile offen sind. Die elektrische Leistung Aus dem Amateurfunklehrgang Klasse E wissen Sie, dass Leistung das Produkt ist aus Spannung und Strom. Für Wechselspannung/Wechselstrom an einem Widerstand gilt diese Formel auch, wenn entsprechende Effektivwerte eingesetzt werden. Die Formel gilt nicht, wenn die Last Kondensatoren oder Spulen enthält. Dann treten Phasenverschiebungen zwischen Spannung und Strom auf, die bei der Berechnung der Leistung berücksichtigt werden müssen. Die Berechnung wird schwierig. Dies ist nicht Gegenstand der Prüfung für das Amateurfunkzeugnis. Nur eine Frage ist enthalten, nämlich die Leistung zu berechnen, wenn nur ein Kondensator angeschlossen ist. Ein Kondensator wird bei Wechselstrom nur kurz aufgeladen und dann wieder entladen und danach umgekehrt aufgeladen. Dabei wird keine Leistung abgegeben. Der Kondenstor gibt diese immer wieder zurück. Nur ganz geringe Umladeverluste entstehen, die praktisch vernachlässigbar sind. Prüfungsfrage:
Kommentar: Siehe Absatz oberhalb!
Es sind viele Aufgaben zum Thema Leistung im Prüfungsfragenkatalog enthalten, wobei alle umgestellten Formeln in der Formelsammlung stehen. Man muss wissen, dass Belastbarkeit eines Widerstandes maximale Leistung bedeutet. Prüfungsfrage:
Lösung machen? Bitte melden!
Prüfungsfrage
Tipp für TC108: Belastbarkeit ist die maximale Leistung für einen Widerstand. Stellen Sie die Formel P = I2 · R nach I um, wie es in der Lektion 1 gezeigt wurde. Setzen Sie hier die Leistung in Watt und den Widerstand in Ohm ein, damit der Strom in Ampere herauskommt.
Prüfungsfrage
Tipp für TC111: Sie müssen den Spitze-Spitze-Wert zunächst durch 2 teilen, um den Spitzenwert zu erhalten und dann mit 0,7 multiplizieren, um daraus den Effektivwert zu berechnen. Also: Der Spitzenwert ist 25 V geteilt durch 2, also 12,5 V. Der Effektivwert der Spannung ist 12,5 V mal 0,7 also 8,8 V. I gleich U durch R, also 8,8 V geteilt durch 1 kΩ gleich 8,8 mA. Prüfungsfrage:
Prüfungsfrage:
Lösung: Wie TB914 oder einfach so: I = 2 A. 2 A mal 100 V = 200 W.
Prüfungsfrage:
Lösungsweg: Auch hier ist einfaches Kopfrechnen angesagt. Da alle Widerstände gleich groß sind, nehmen sie alle die gleiche Leistung auf. Das ergibt zusammen elf mal fünf Watt, also 55 W.
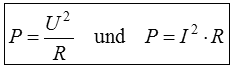
Leistungsformel umstellen Es folgen drei Aufgaben, bei denen die Leistungsformel
Prüfungsfrage
Kommentar: Siehe Lektion 1!
Prüfungsfrage:
Kommentar: Siehe Lektion 1!
Prüfungsfrage:
Kommentar: Siehe Lektion 1!
Prüfungsfrage:
Tipp zu 105 und 106: Sie müssen die Formel P = U2 / R nach U umstellen, wie es in der Lektion 1 gezeigt wurde. Wenn dieser berechnete Spannungswert geringer ist als die gegebene Spannungsfestigkeit, ist dies die Lösung. Lösung machen?
Prüfungsfrage:
Lösung machen? Die Formel für U steht in TB923 weiter oben.
Prüfungsfrage:
Lösungsweg: Hier braucht man nicht lange zu rechnen. Die Überlegung ist, mit wie viel (A) muss man die 12 (V) multiplizieren, damit 48 (W) herauskommt, denn P = U . I.
Prüfungsfrage:
Lösungsweg: Der Wirkungsgrad eines HF-Verstärkers berechnet sich aus dem Verhältnis von abgegebener Wechselstromleistung (Ausgangsleistung) zu aufgenommener Gleichstromleistung. Die aufgenommene Gleichstromleistung beträgt
Prüfungsfrage:
Lösungsweg: Prozentrechnung! Wenn beide Messgeräte einen um 5 % zu niedrigen Wert anzeigen, also nur 95 %, sind es zweimal 95 %, also 90,25 % oder insgesamt bei der Leistung 100 minus 90,25 gleich 9,75 %.
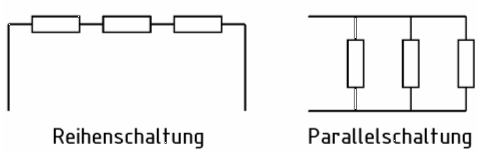
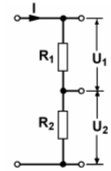
Reihenschaltung von Widerständen Im Lehrgang für Klasse E wurden in der Lektion 4 recht ausführlich die Reihen- und Parallelschaltung von Widerständen, sowie einfache gemischte Schaltungen und deren Berechnung behandelt. Allerdings waren es einfachere gemischte Schaltungen als manche hier aus dem Fragenkatalog für Klasse A. Hier noch einmal die Übersicht: Bei einer Reihenschaltung sind die Widerstände hintereinander geschaltet. Der Gesamtwiderstand ist ganz einfach die Summe der Einzelwiderstände. Ferner wissen Sie aus der Lektion 4 Klasse E, dass sich bei einer Reihenschaltung die Spannungen wie die Widerstände verhalten. Ist bei einer Reihenschaltung ein Widerstand beispielsweise fünfmal so groß wie ein anderer, muss auch die Spannung an diesem Widerstand fünfmal so groß sein. Prüfungsfrage:
In einer Reihenschaltung verhalten sich die Spannungen wie die zugehörigen Widerstände, also Parallelschaltung von Widerständen Die Formel für die Parallelschaltung von Widerständen lautet Wenn nur zwei Widerstände parallel geschaltet sind, vereinfacht sich die Formel zu Wie in der vorigen Lektion gezeigt wurde, lässt sich diese Formel auch umstellen zu Mit welcher der beiden Formeln gerechnet wird, ist "Geschmacksache". Wenn man einen Taschenrechner mit 1/x-Taste hat, ist die obere Formel einfacher zu handhaben. Dies zeige ich Ihnen am Beispiel der Prüfungsaufgabe TD103. Prüfungsfrage:
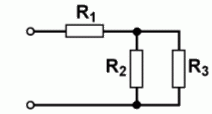
Zunächst Berechnung der Parallelschaltung von R2 und R3. Lösungsweg 1 mit der oberen Formel: Ich lasse die Einheit einfach weg, da sie in beiden Fällen gleich ist. Darauf müssen Sie aber immer achten! Mit dem Taschenrechner geben Sie ein. Machen Sie mit! Der Ersatzwiderstand beträgt also 4,0 kΩ. Lösungsweg 2: Mit der unteren Formel rechnet man Natürlich muss dasselbe heraus kommen, wenn die Formeln richtig sind. Zu diesen 4,0 kΩ kommen noch die 3,3 kΩ von R1 hinzu und es ergibt sich der Gesamtwiderstand zu 7,3 kΩ.
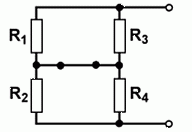
Prüfungsfrage:
Tipp: Auch hier sind die oberen beiden parallel geschalteten Widerstände gleich groß (zusammen also halb so groß) und die unteren beiden ebenfalls.
Wenn drei Widerstände parallel geschaltet sind, rechnet man nach der Formel obwohl es auch eine nach R aufgelöste Formel für drei Widerstände gibt. Sie lautet Prüfungsfrage:
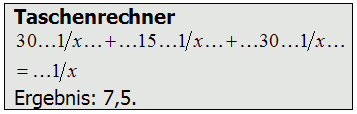
Erster Lösungsweg nur für die Parallelschaltung der drei Widerstände: Zweiter Lösungsweg: Wenn Sie wollen, überprüfen Sie einmal die Richtigkeit der zweiten Formel für die drei Widerstände. In der Prüfungsaufgabe TD122 liegt dazu noch ein 2,7-kΩ-Widerstand in Reihe, so dass sich ein Gesamtergebnis von 10,2 kΩ ergibt. Dritter Lösungsweg: Man kann auch erst zwei beliebige Widerstände zu einem Ersatzwiderstand zusammenfassen und dann zu diesem Ersatzwiderstand den dritten parallel schalten. In diesem Fall kann man die zwei gleichen Widerstände von je 30 kΩ zu 15 kΩ zusammenfassen und dazu wiederum den dritten Widerstand von 15 kΩ parallel schalten, wodurch sich auch 7,5 kΩ ergeben.
Prüfungsfrage:
Lösung: 12 und 12 parallel sind 6, 6 parallel sind 3, 1,5 in Reihe ergibt 4,5
Prüfungsfrage:
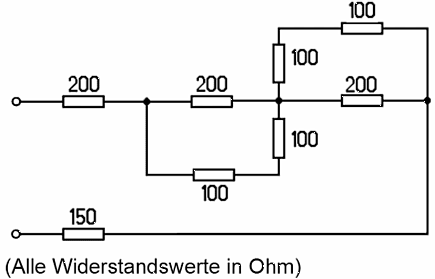
Tipp: Bei drei gleichen Widerständen ist jeder Einzelwiderstand dreimal so groß Gemischte Schaltungen Bei gemischten Schaltungen von vielen Widerständen gilt folgendes Prinzip. Suchen Sie zunächst die Widerstände heraus, die entweder eindeutig in Reihe oder eindeutig parallel geschaltet sind und ersetzen Sie diese durch den berechneten Ersatzwiderstand. Prüfungsfrage:
Lösungsweg: In Aufgabe TD107 müssen Sie zunächst die beiden 100-Ω-Widerstände durch je
200
Ω ersetzen und diesen dann zum 200-Ω-Widerstand parallel schalten. Dies ergibt je
100
Ω.
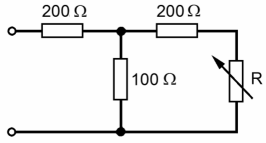
Prüfungsfrage:
Lösung: Wenn R kurzgeschlossen wird, liegen die 200 Ω und die 100 Ω parallel und ergeben 66,7 Ω. Plus 200 Ω ergeben sich 266,7 Ω. Bei Leerlauf ist der 200-Ω-Widerstand wirkungslos. Die 200 Ω und die 100 Ω liegen in Reihe und ergeben 300 Ω.
Prüfungsfrage:
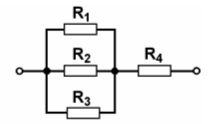
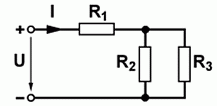
Lösungsweg: Aufpassen! Es ist nicht der Gesamtstrom gefragt, sondern der Teilstrom durch einen der beiden parallel geschalteten Widerstände, in diesem Fall der Strom durch R3. Nun ist es in diesem Spezialfall insofern einfach, weil sich der Gesamtstrom je zur Hälfte auf die beiden gleich großen Widerstände aufteilt. Um den Gesamtstrom zu berechnen, benötigen wir zunächst den Gesamtwiderstand. Er setzt sich zusammen aus der Parallelschaltung von R2 und R3 plus der Reihenschaltung von R1. Damit berechnet sich der Gesamtstrom zu und damit beträgt der Teilstrom durch R3 die Hälfte davon, also 0,5 mA.
Prüfungsfrage:
Lösungsweg: Diesmal ist nach der Leistung an dem Teilwiderstand gefragt, also brauchen wir außer dem Strom noch die Spannung. Da alle Werte mit denen der Aufgabe TD112 übereinstimmen, können wir die Teilergebnisse von oben übernehmen. Wenn man den Strom an einem Widerstand kennt, kann man entweder direkt mit der entsprechenden Leistungsformel oder auf dem Umweg über die Spannung die Leistung berechnen. Direkter Weg: Indirekter Weg:
Prüfungsfrage:
Lösungsweg: Wenn durch R3 ein Strom von 1 mA fließt, beträgt der Strom durch R2 ebenfalls 1 mA. Damit ist der Gesamtstrom 2 mA. Der Gesamtwiderstand beträgt 15 kΩ, (Siehe Aufgabe TD112 weiter oben). Damit beträgt die Gesamtspannung 15 kΩ mal 2 mA gleich 30 Volt.
AnhangDieser Online-Lehrgang wurde mit freundlicher Genehmigung des Autors aus seinem Buch für das Internet umgewandelt.
Dieser Lehrgang basiert auf dem Prüfungsfragenkatalog vom 28. Februar 2007 der Bundesnetzagentur (BNetzA). Alle darin vorkommenden Themen wie Grundlagen der Elektrotechnik, Elektronik sowie Sender- und Empfängertechnik, Übertragungstechnik, Antennentechnik und Messtechnik aus dem Gebiet "Technische Kenntnisse" werden ausführlich erläutert. Die Erfahrung mit praktischen Lehrgängen wird genutzt, um den Prüfling in die Lage zu versetzen, jede Frage aus dem Fragenkatalog richtig zu beantworten. Dieses Buch ist auch sehr gut für das Selbststudium geeignet. Dieser Lehrgang baut auf dem Lehrgang für die Klasse E auf. Sie sollten also erst den Lehrgang für das Amateurfunkzeugnis Klasse E durchgearbeitet haben oder zumindest bei Verweisen dort nachlesen können.
*) Wenn Sie noch im vor dem 1. Juni die Prüfung Klasse A (nach dem alten
Fragenkatalog Klasse 1+2) machen wollen, sollten Sie sich dieses Buch besorgen,
denn es wird in Kürze ausverkauft sein. Bis Ende Mai wird noch nach altem
Fragenkatalog geprüft.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
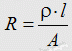
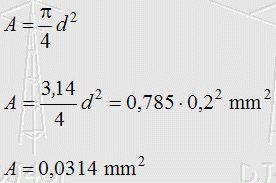
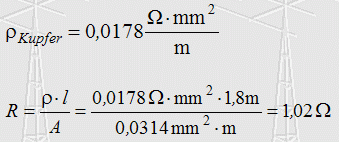

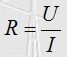 oder umgestellt
oder umgestellt
 x
x